机器学习——Overfitting
Overfitting(过拟合)是机器学习中可能最让人头疼的问题了。对应Overfitting的是Underfitting(欠拟合),相比之下戏份就少了很多。
简单来说,Underfitting,是$E_ {in}$高,$E_ {out}$也很高。于是人们会想方设法地减少$E_ {in}$,认为这样就可以得到较好地结果。但是不幸的是,有时候$E_ {in}$已经很低了,这个模型依然有很高的$E_ {out}$.这就很让人头疼。这就是overfitting。想要更好的解决Overfitting,理解一些数学理论如VC dimension是很有帮助的,给我们提供了更多出现这种情况的原因和解决的思路。
其实Overfitting我们之前也早有提及过。
首先来看一下overfitting的简单的例子:
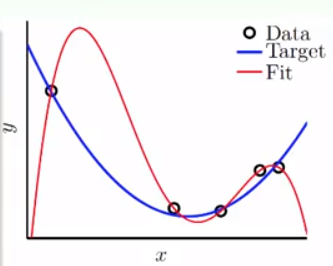
对于目标函数产生的资料,加上了一点noise,在训练集样本很少的情况下,出现了上面的情况:目标函数的$E_ {in}$,比我们得到的这个与目标函数差了十万八千里的函数的$E_ {in}$更大。我们的算法选择的是$E_ {in}$最小的,因此就选择了表现很差的模型。
从上面的样例我们想到了nonlinear transform,当我们进行特征转换的时候,vc dimension大大增加,使得付出的代价变得很高,在样本不够的情况下,很容易得到很差的$E_ {out}$,这就是一种overfitting.于是又一次看到了这张图。

当然,造成上面的结果有一点原因是噪声,但是即使没有噪声,最多最多,他们的$E_ {in}$也是一样的,而且实际中,没有噪声的情况是很少出现的。这说明了造成overfitting的两个原因:1.noise过多。很好理解,更好的适应了noise,它的泛化能力当然不行;2.使用过于复杂的模型,去估计较为简单的目标函数。一般来说,简单的函数只是复杂模型的特例,而且因为噪声的原因往往目标函数不能完美拟合,但是复杂的模型就能做的非常完美。但是另一方面,它的泛化能力也大大下降了。
如果我们采用复杂的模型估计复杂的函数呢?在我们心里可能会想,这下总会好点了吧。因为复杂的目标函数,你不用复杂的模型,根本就不可能完美地估计出来。似乎有点道理,我们来看下面地例子:
用10次的多项式产生一些数据,加上噪声。我们分布用10次的$H$与2次的$H$来对它进行拟合:
目标函数:

拟合结果:

通过对比,我们惊奇地发现,二次的拟合结果,虽然$E_ {in}$做得不如,但是$E_ {out}$比10次的更好!
如果我们使用二次的多项式,那首先我们不可能做到完美,但是我们发现,有时候它的表现比更复杂地模型模拟的更好,尽管原来的模型非常地复杂。
想要了解这其中的原因,我们来观察一下两个$H$的learning curve:
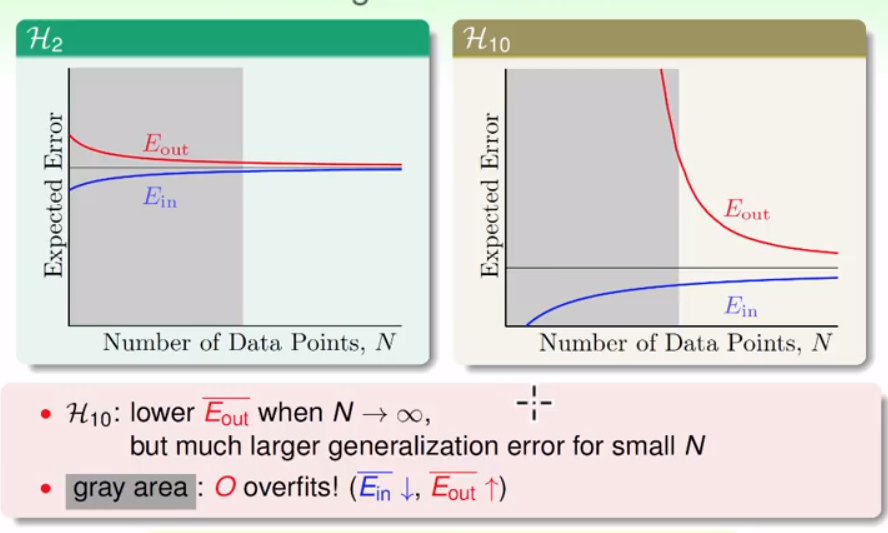
对于右侧的我们是熟悉的,观察右侧的$H_ {10}$的学习曲线,我们发现,虽然当N区域无穷的时候,它有更好的性能,但是在灰色区域里,它是Overfitting的。因此,overfitting的最关键的原因:数据量不够多。
因为模型越复杂,可以走的路就越多,在资料量小的时候,可能很多条路都会完美走过这条道,而其他的部分可能差的很远。这依然可以用VC dimension来解释,代价太大了,为了降低代价,必须需要更大的N.
当然,上面的例子中依然有noise的存在。Noise或多或少影响了复杂模型的性能,而且越复杂模型它的影响可能越大。对于没有noise的模型,是否还有上面的结果?
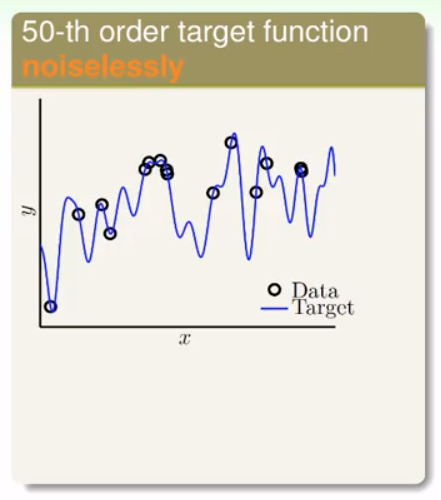
利用50次目标函数产生的数据,依然用$H_2$与$H_ {10}$去模拟:
目标函数:
拟合结果:
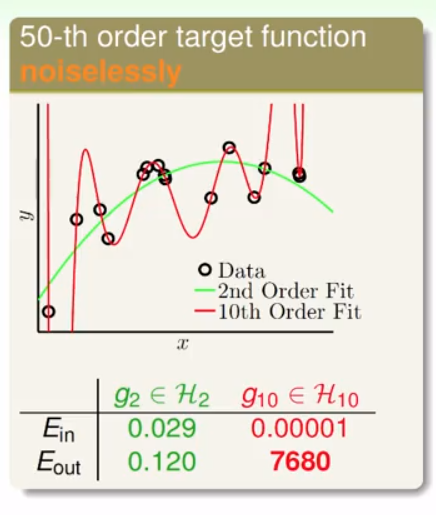
可以看到二次函数依然比10次函数表现得更好。原因和上面一样。所以没有很多数据量的支撑,使用较为简单的模型往往效果更好。
这时候我们会纳闷,这明明没有noise啊,为什么会这样?过于复杂的模型与简单的假设似乎带来了和noise类似的结果。
在机器学习领域中,对于过于复杂的模型本身带来的类似于noise的效果,被称为Deterministic Noise.
对于普通的noise,我们假设为高斯噪声(Gaussian Noise)。对于Gaussian Noise与Deterministic Noise对于模型的影响,$Q_f$为目标函数的次数,那么可以用下面的图来形象展示出来:
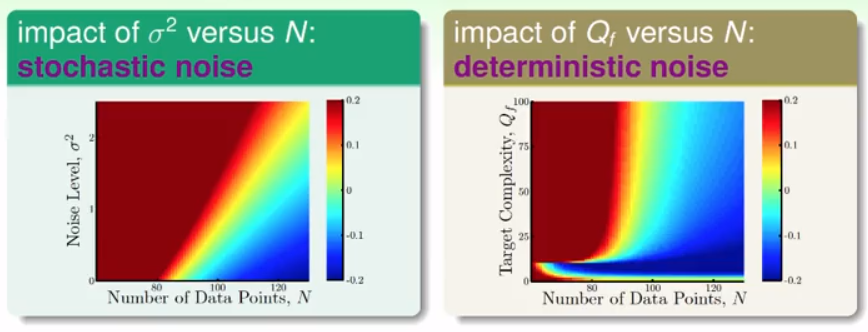
可以看出来,两种噪声带来的效果相近,可以通过增加N来避免过拟合的情况。
值得注意的是,右侧图中,左下角依然有一块会过拟合。需要注意,上述图中$H$的次数是不变的,因此,如果$Q_f$小于$H$的次数,会出现第一种情况,power过强的情况.
实际上,deterministic noise与电脑产生伪随机数的原理很相似,过于复杂的模型,造成了随机噪声的效果。
总结一下,Overfitting出现的原因:
1.N太小
2.Stochastic(Gaussian) Noise
3.Deterministic Noise
4.Too Much Power
如何对付overfitting是个很复杂的话题。首先直观来说,降噪,增加样本。降噪,可以通过修正label与去除错误的样本来实现,而增加样本往往没有那么容易,某些情况下我们可以自己创造data.另外还有两种比较复杂的做法,也有很好的效果:Regularization 与 Validation.以后会专门写博客来介绍。