数字图像处理——图像压缩
我们生活中用到很多图像,也见过很多图像格式,实际上大部分见到的都是压缩格式。说压缩技术改变了世界一点也不为过。这篇文章简单介绍一下图像压缩的一些基本内容。
对于一张$512\times 512$的图片,如果每个像素需要8bit,那么这张图有2Mb大,而如果一个RGB视频,每秒30帧,那么需要网络速率大小是180Mb/s。而且这个图片的质量也并不高,只有$512\times 512$。因此我们可以看到压缩的重要性。压缩分为有损压缩与无损压缩。下面是几个常见的图片压缩格式:

下面我们说明几个基本的定义:$n_1,n_2$分别代表两张图$x_1,x_2$的大小(更正式的说法,是包含信息的单位个数)。那么定义$x_1$相对于$x_2$的数据冗余为:
$$
R_D = 1 - \frac{1}{C_R} = \frac{n_1 - n_2}{n_1}
$$
这里的$C_R$指的压缩比例:$C_R = \frac{n_1}{n_2}$,
$$
C_R \in [0,\infty),R_D \in (-\infty,1].
$$
这个比较的前提是信息量一致。如果$n_2$是压缩后的,因此会出现情况可能有下面几种:
- $n_2 >> n_1$,压缩很失败,$R_D = -\infty,C_R = 0$,说明冗余过多,实际上只要$n_2 > n_1$,那么压缩就失败了,$R_D<0,C_R < 1$。
- $n_2 = n_1$,相当于没有压缩,$R_D = 0, C_R = 1$。
- $n_2 << n_1$,压缩成功,$R_D = 1,C_R = \infty$,实际上只要$n_2< n_1$,压缩就有效果,这时候$R_D > 0,C_R > 1$。
一般来说在数字图像中有下面3种基本的冗余:
- 编码冗余,指的是编码上不需要这么多的字长。
- 像素间的冗余,比如相邻像素可能是一样的或者近似,有某种规律,可以用更简单的方式表示,这就是像素之间的冗余。
- 视觉冗余,人的视觉没有太高的敏感度,比如颜色太相近人眼无法区分,或者图片略缩图比较小,不需要太多的灰度值来表示,又或者人眼对对比度光照等等更敏感,可以适当加大颜色的压缩比例等等。
对于编码冗余以及像素间的冗余,对应的是无损压缩的解决方案,而视觉冗余,则会损失图片质量,但是好的压缩方法会在压缩比例很大的情况下尽可能的保存更多的图片视觉信息。
编码冗余
解决编码冗余的方法可以使用霍夫曼编码,这个之前在信息论中有提到:Huffman编码。
霍夫曼编码是无损压缩方法,除此以外还有很多别的编码方法,主要还是针对与像素出现的概率与熵。下面举个编码例子:
用$L_ {avg}$表示一张图片各个像素的平均码长,那么平均码长计算如下:
$$
L_ {\mathrm{avg} }=\sum_ {k=0}^{L-1} I\left(r_ {k}\right) p_ {r}\left(r_ {k}\right)
$$
下面是一个只有8个灰度值的图片进行熵编码的示意(code 1普通编码,code 2熵编码):

第一种编码方案,对每个灰度值都进行3bit的编码。
这时候计算得到平均码长为:
$$
L_ {\mathrm{avg} }=\sum_ {k=0}^{8-1} /\left(r_ {k}\right) p_ {r}\left(r_ {k}\right) = 3 \text{bits}.
$$
第二种利用概率进行熵编码,对经常出现的灰度值给较短的编码,而对很少出现的灰度值给予较大的编码,这时候得到的平均码长为:
$$
L_ {\mathrm{avg} }=\sum_ {k=0}^{8-1} l_ {2}\left(r_ {k}\right) p_ {r}\left(r_ {k}\right) = 2.7 \text{bits}.
$$
可以看到这个图片可以被压缩,压缩比例以及相对冗余如下:
$$
C_ {R}=\frac{n_ {1} }{n_ {2} }=\frac{3}{2.7}=1.11\ R_ {D}=1-\frac{1}{C_ {R} }=1-\frac{1}{1.11}=0.099
$$
像素间的冗余
对于像素间的冗余,举个例子如下图:
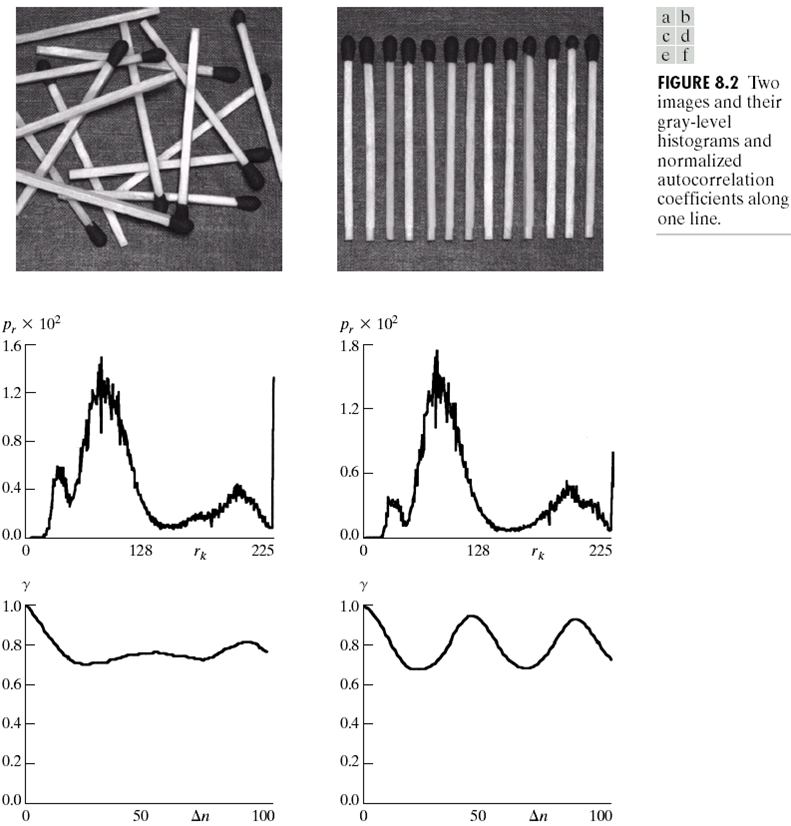
这两张图片有着相同的直方图,但是很明显右侧的图片更有规律。我们可以利用空间位置的规律来对其进行压缩。最后两幅图是关于像素间相关系数的定义。这里定义一个相关系数如下:
$$
\gamma(\Delta n)=\frac{A(\Delta n)}{A(\Delta n=0)}
$$
上式中:
$$
A(\Delta n)=\frac{1}{N-\Delta n} \sum_ {y=0}^{N-1-\Delta n} f(x, y) f(x, y+\Delta n)
$$
$\Delta n$是像素间的距离,可以理解为步长。我们对$\Delta n$内的像素进行另一种形式的压缩。
可以看到,在$\Delta n = 1$时,$\gamma_1 = 0.9922,\gamma_2 = 0.9928$,意味着当像素距离为$1$时,两张图片的相关系数都很高,而当$\Delta n = 45, 90$时候,图二的相关系数依然很高。有着很高的相关系数,意味着可以更好的压缩。但是需要注意一点,当$\Delta n = 1$时,几乎所有图片都有比较高的相关系数,但是$\Delta n$间隔太小,意味着最后压缩比例不会很大。因此想要很好的压缩需要在$\Delta n$比较大的情况下有比较高的相关系数,我们肉眼也可以看到,上述两张图中第二张图更规律,可以更好地被压缩。具体的压缩过程需要一个过程,叫做可逆映射(reversible mapping)。
这个压缩过程也很简单,就是依据一个路线扫描图像:
$$
f(x, 0), f(x, 1), \ldots, f(x, N-1)
$$
将结果存为类似下面的序列:
$$
\left(g_ {1}, w_ {1}\right),\left(g_ {2}, w_ {2}\right), \dots
$$
$g_ {n}$表示像素值,而$w_ {n}$表示像素值连续出现的长度。这个方法有点像字典压缩算法。下面是一个例子:

对于第100行,每个灰度值需要1bits,而长度需要10bits来存储,那么序列对:
$$
(1,63)(0,87)(1,37)(0,5)(1,4)(0,556)(1,62)(0,210)
$$
只需要88bits,而原本的图像需要1024个bits。对于整个图片,只是用12166对类似的表示就可以存储,而原图大小为$1024\times 343$。这样的情况下,压缩比例与冗余指数分别为:
$$
\begin{aligned} C_ {R} &=\frac{n_ {1} }{n_ {2} }=\frac{(1024)(343)(1)}{(12166)(11)}=2.63 \ R_ {D} &=1-\frac{1}{C_ {R} }=1-\frac{1}{2.63}=0.62 \end{aligned}
$$
视觉冗余
视觉冗余对应有损编码,但是有时候一些信息量的损失对于人眼来说几乎是察觉不到的,如下图的例子:

后面两种方法使用了不同的quantization方法,最后压缩的图片大小一致,但是第二种明显优于第一种。对于有损编码,需要一个衡量压缩后图片好坏的标准。常用的损失函数有下面两种:
- root mean square error: $$e_ {\mathrm{rms} }=\left[\frac{1}{M N} \sum_ {x=0}^{M-1} \sum_ {y=0}^{N-1}[\hat{f}(x, y)-f(x, y)]^{2}\right]^{\frac{1}{2} }$$
- mean square signal-to-noise ratio: $$S N R_ {\mathrm{MS} }=\frac{\sum_ {x=0}^{M-1} \sum_ {y=0}^{N-1} \hat{f}(x, y)^{2} }{\sum_ {x=0}^{N-1} \sum_ {y=0}^{N-1}[\hat{f}(x, y)-f(x, y)]^{2} }$$
另外就是人的主观评判了。
关于有损压缩,这里也不会介绍过多的算法内容。有损压缩对应的有Predictive以及transform,也就是一个是靠预测,存储的是空间差异,类似于上面介绍的像素间冗余,而transform会转换到另外的一个domain,比如快速傅里叶变换(FFT)或者离散余弦变换(DCT)。在压缩中,使用更多的是DCT,DTF与DCT对比如下:

可以看到在root mean square error上,DCT有更好的表现。具体的算法过程想要了解的可以去查询更详细的文章等。实际上,最著名的图片编码JPEG就是用到了transform,下面是压缩效果:

而对于JPEG 2000,是JPEG的改进,有更好的压缩效果。但是一般来说更好的压缩效果也意味着更长的压缩时间:

对于有损压缩,这里介绍的是非常少的一部分内容。实际上实现压缩的方法还有很多,比如奇异值分解,我们知道奇异值分解会根据奇异值保存不同重要程度的组成成分,这也延伸到很重要的机器学习算法主要成分分析PCA,只要保存几个主要的成分就可以保留矩阵的大部分内容,从而对数据进行降维,大大减少占用内存等,可以看这个知乎的回答:奇异值分解的物理意义是什么?。也可以使用奇异值分解,对图片进行压缩。关于奇异值介绍可以看之前的博客:SVD与EVD。
视频压缩
视频编码和压缩实际上与图像相关很大,但是视频可以有更高的压缩比例,因为视频是连续动态的,而临近帧之间可以做动作估计。关于视频的压缩编码以及动作估计这里放上补充材料,有兴趣的可以下载了解更多: video coding, motion estimation。