数字图像处理——图像分割
搞计算机视觉的都知道图像分割的重要性,是物体,语义识别的基础。segmentation也是一个很热门的方向,除了二维上的图像分割,还有三维的物体分割。今天来学习一些图像分割的基础。
实际上图像分割与边提取算法很相关,因为我们要分割一副图,实际上就是利用边界来分割。因此边提取,锐化,滤波等等是图像处理的基础,而图像分割,目标检测等等,都会用到先前的知识来做基础或者预处理。
下面的是图像分割的一个例子:

图像分割的难点在噪声情况下的robustness以及多种特征的组合。一般来说图像分割是几乎所有计算机视觉应用的第一步。
图像分割就像是分类,它的标准有两条:1,同一个分割区域要尽量相似,2,不同的分割区域需要尽量的不连续,相差较远。对于灰度图的不连续性,我们倾向于去找图片中的点,直线,与边界。下面介绍如何在图中探测点,直线,以及边界。
Point Detection
实际上,说到这里,我们应该注意到某种程度上,图像分割的目标与边检测是有很大相似性的。而对于点的检测,我们直到点是没有方向的,因此可以想到使用没有方向的边界探测,就能很容易找到点,当然也很容易想到了Laplacian算子。对于点检测,可以使用下面的式子:
$$
g(x, y)=\left{\begin{array}{ll}{1} & {\text { if }|R(x, y)|>T} \ {0} & {\text { otherwise } }\end{array}\right.
$$
上式中$T$是一个阈值,而$R(x,y)$是经过拉普拉斯滤波后得到的值。
Line Detection
直线的探测与边探测不同的地方在于我们想要探测的是直线,而不是随意形状的边。直线的探测与点探测相比就会更加复杂,因为它是有方向的。下面是水平垂直以及45°方向的sobel滤波器:
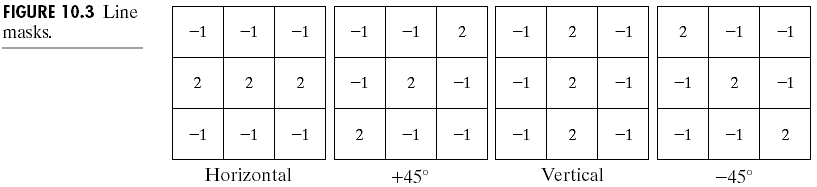
那么,对于任意方向的直线如何探测呢?有个想法是,对于直线探测比较复杂,但是点的探测是很简单的。有没有什么方法,将直线的探测转换成点的探测?对于直线,我们直到它的参数表达式为:
$$
y^{\prime}=m x^{\prime}+c
$$
因此,任何一条直线,对应一对参数,也就是参数域的一个点。因此,对于直线的探测,可以转化成参数域上点的探测。这个想法延伸出来的算法叫做Hough Transform。使用Hough Transform的边探测算法如下:
- 先建立一个二维的矩阵,横纵分布代表$(m,c)$,步长需要自己确定
- 初始化这个矩阵为0
- 对于图像中某个像素,对二维矩阵中每一对参数进行计算,看点是否在对应的直线上,如果在,矩阵这个位置的值+1。
- 根据阈值判断矩阵中符合要求的参数点,来得到对应的直线
当然,具体的实现细节有更多需要注意的地方,比如对于图像中像素,我们首先可能需要利用sobel算子进行Edge detect,等等,对于可能是直线的像素探测出来。否则对于一张空白的图片,每个像素也没必要计算。初次之外对于$m,c$等,我们可以使用极坐标下的$\rho,\theta$等等来替换,这里有一个Hough Transform的补充材料,有需要可以仔细阅读一下:Hough Transform。
Edge Detection
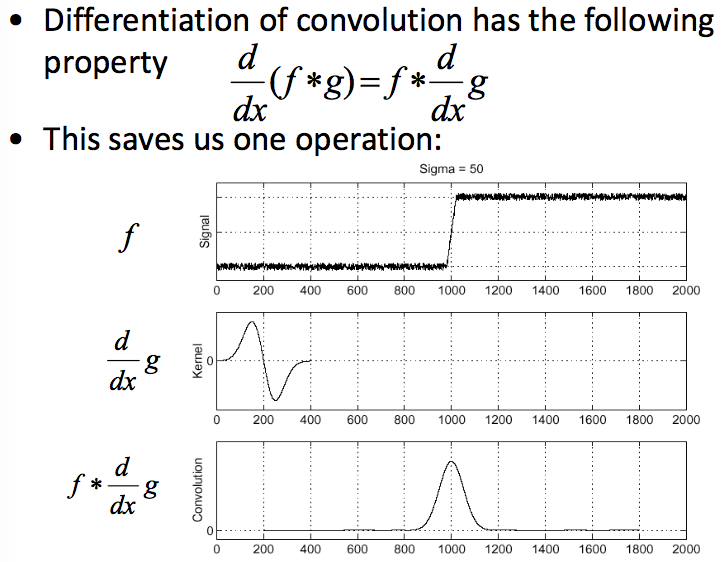
边探测,实际上之前已经提到了不少,因此这里就简单说明一下。边探测算法很多,有从一节梯度推到的sobel算子等,还有二阶的拉普拉斯算子,还有更常用的之前说的Canny边探测算法。而一般来说边探测算法都需要用到高斯滤波,平均滤波等低通滤波器来进行噪声平滑,因为梯度边探测以及拉普拉斯算子对于噪声都非常敏感,如下图:
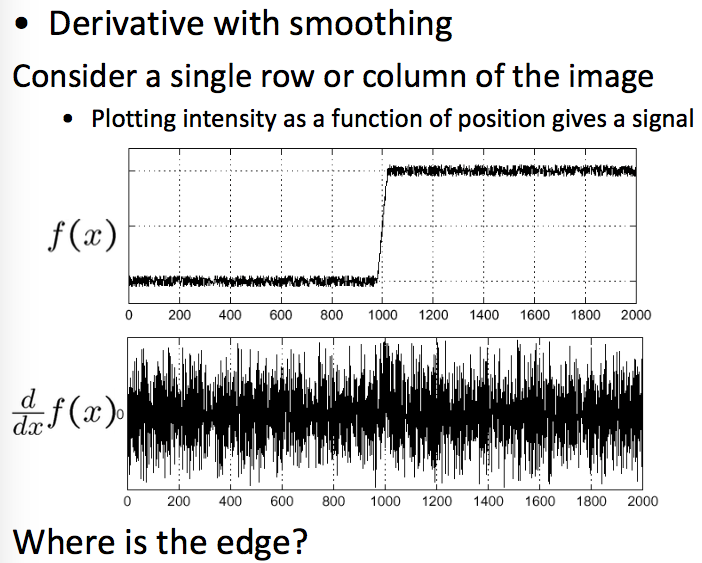
这个不难理解,因为噪声变化也总是比较突兀,而梯度以及拉普拉斯在频域都是高通滤波器,对这样的噪声是非常敏感的。因此需要使用高斯滤波来进行平滑:
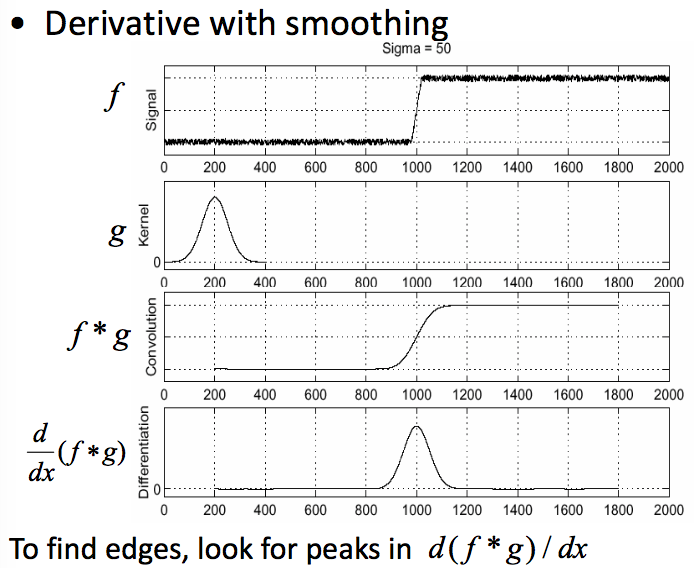
下面是几个边探测的效果图:

加上平均滤波(或者高斯滤波),使得我们想要的边更加明显:

此外,通过上面的算法检测到的边,还是直线,总会出现断掉的情况,因为噪声等等原因,这些是无法避免的。如果想要让它们连接起来,需要进行别的处理,可选的有局部的以及全局的连接方法。

补充(thresholding based segmentation)
上述说明的,是一些通过边,直线等探测算法,实现图像的分割,这里补充一点基于阈值的图像分割,将灰度图转换成二值图,从而根据简单的黑白来分割。根据阈值分割的,一般有3种做法。
一般来说我们想要得到的分割结果如下:
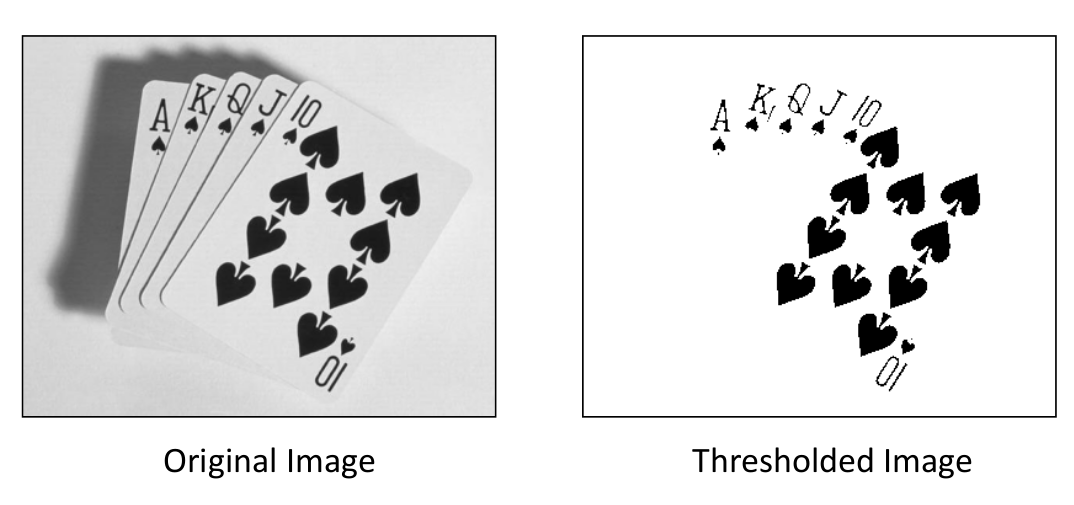
阈值选择不好就会出现下面的情况:
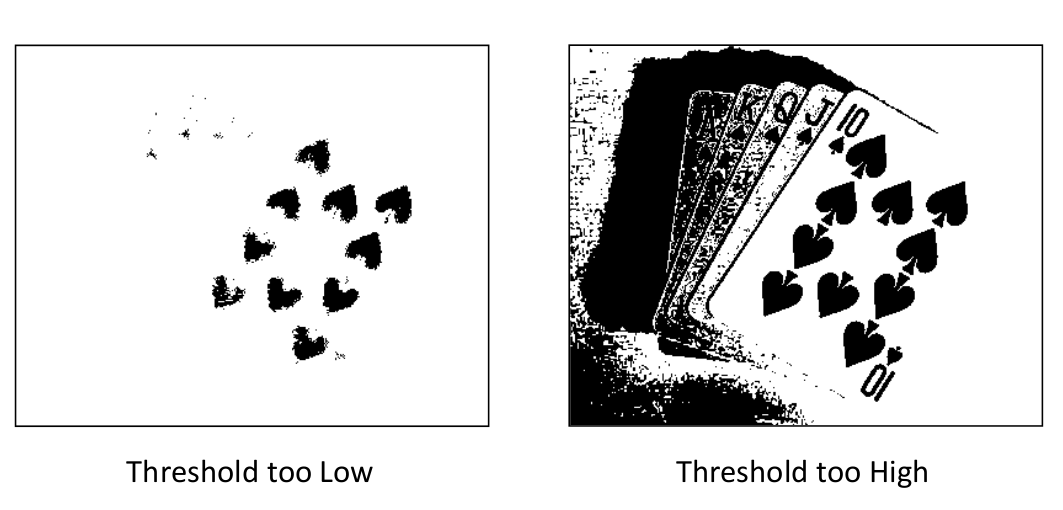
Basic Global Thresholding
最基本的全局阈值算法是最简单的阈值,使用的是全局阈值,也就是我们根据观察图片的直方图,如果需要被分割的两个部分在直方图上有明显的表现趋势,阈值的选择就会简单很多,如下图,第三种情况,我们无法直接看出最优的阈值应该在哪里:
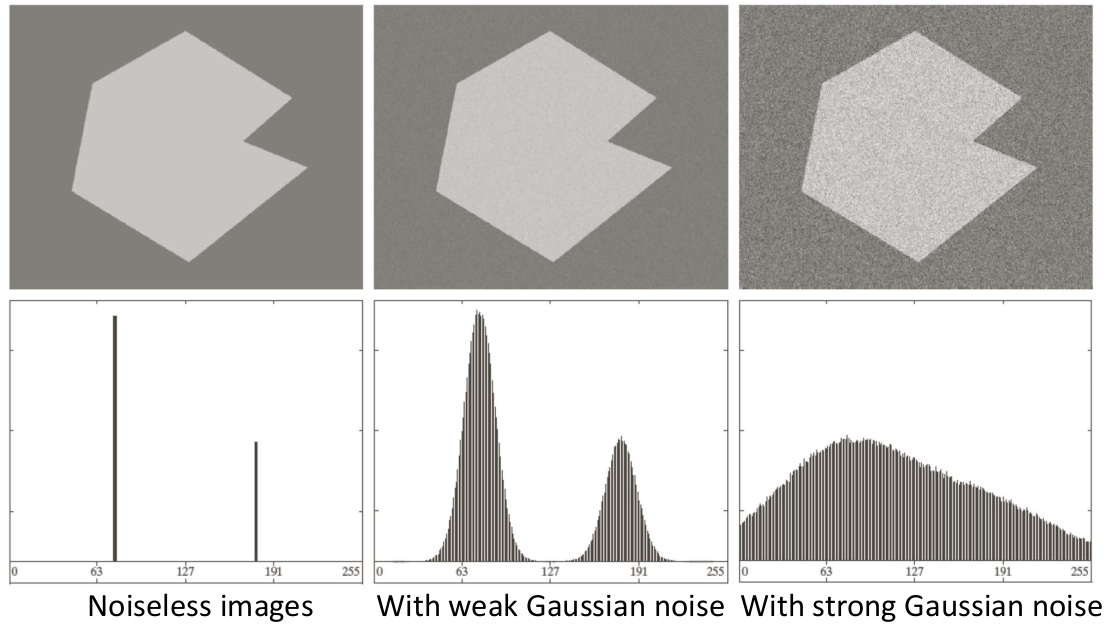
对于全局阈值的算法确定如下:

首先确定一个阈值初始值,然后计算根据这个阈值得到的两个类各自的灰度均值$m_1,m_2$,在对这两个均值求平均得到下一个阈值,不断迭代直到当前阈值与上一个阈值的变化量小于一定量,我们认为收敛了。这个算法有点类似于k-means聚类。下面是一个例子:
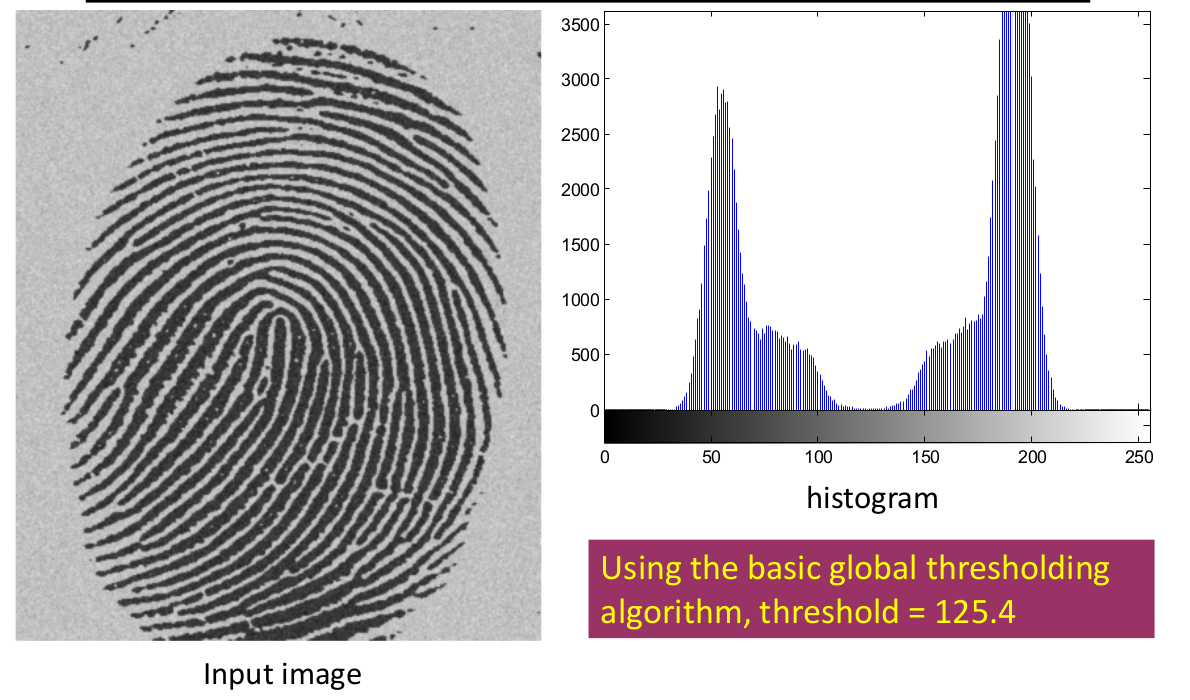

Otsu’s Optimum Global Thresholding
最基本的得到的往往不是最佳的。实际上上述说的算法很依赖于初始值,不一定会找到最优的点。而Otsu提出的最佳全局阈值算法通过最大化不同类的方差,来找到更好的全局阈值。首先,我们做下面的定义:
- 对直方图进行归一化,使得: $$p_ {i}=\frac{n_ {i} }{M N}, \sum_ {i=0}^{L-1} p_ {i}=1, p_ {i} \geq 0$$
- 阈值变量为$k$,那么$[0,k]$为第一类,而$[k+1,L-1]$为第二类,而$L-1$表示灰度最大值。
- 定义类间方差如下: $$\sigma_ {B}^{2}=P_ {1}(k)\left[m_ {1}(k)-m_ {G}\right]^{2}+P_ {2}(k)\left[m_ {2}(k)-m_ {G}\right]^{2}$$式中$P_ {1}(k)=\sum_ {i=0}^{k} p_ {i}$,为第一类出现的概率,$P_ {2}(k)=1-P_ {1}(k)$为第二类出现的概率,而$m_1(k),m_2(k)$分别是第一类第二类的灰度均值,$m_G$是全局均值。最佳的阈值为:$$ k^{*}=\underset{0 \leq k \leq L-1}{\arg \max } \sigma_ {B}^{2}(k).$$
在matlab中,graythresh计算Otsu最佳阈值。下面是算法效果的展示,可以看到对比第一种方法,它能应对更多的情况:
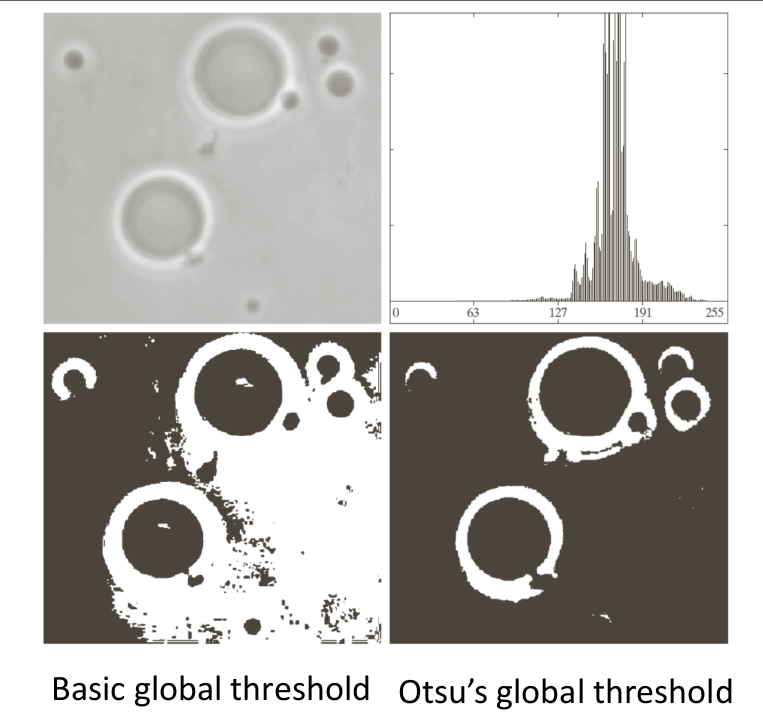
Variable Thresholding——Moving Average
有时候,直接用一个阈值来决定是不可行的。因为光照,阴影等原因,对局部应该选取不同的阈值,这里就使用变化均值,对不同局部区域来做不同的阈值。算法是这样的:
- 加入我们有一个5*5的图片,如下,那么把它重新组织成一个数组的形式:
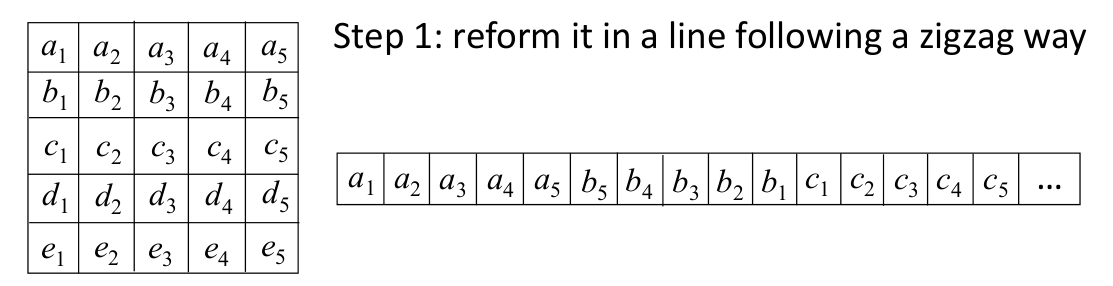
- 对数组中每个位置,进行局部平均,来求得局部阈值,这里选择每4个位置做一个平均:
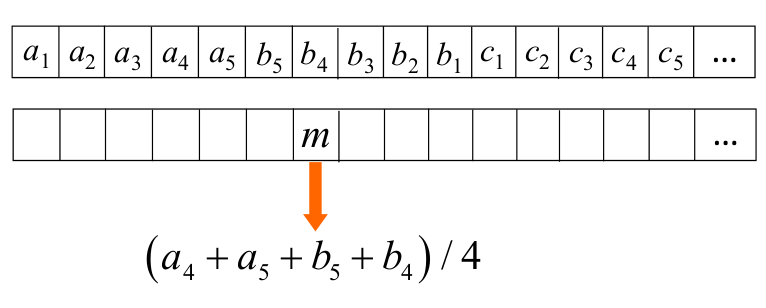
- 将得到的数组,重新组织成matrix的形式,这样得到了“阈值图”$m(x,y)$,根据阈值图,对原图中每个位置的灰度值做下面的处理: $$g(x, y)=\left{\begin{array}{l}{1, \text { if } f(x, y)>K \cdot m(x, y)} \ {0, \text { otherwise } }\end{array}\right.$$得到二值图的分割结果。
这个组织用什么样的顺序应该需要视情况而定,上述描述中是横着走$z$字形状,如果应对别的形状的光照阴影这样是行不通的。也有斜着组织的,能应对更多的case。总之,下面是使用移动平均值算法的效果:
原图: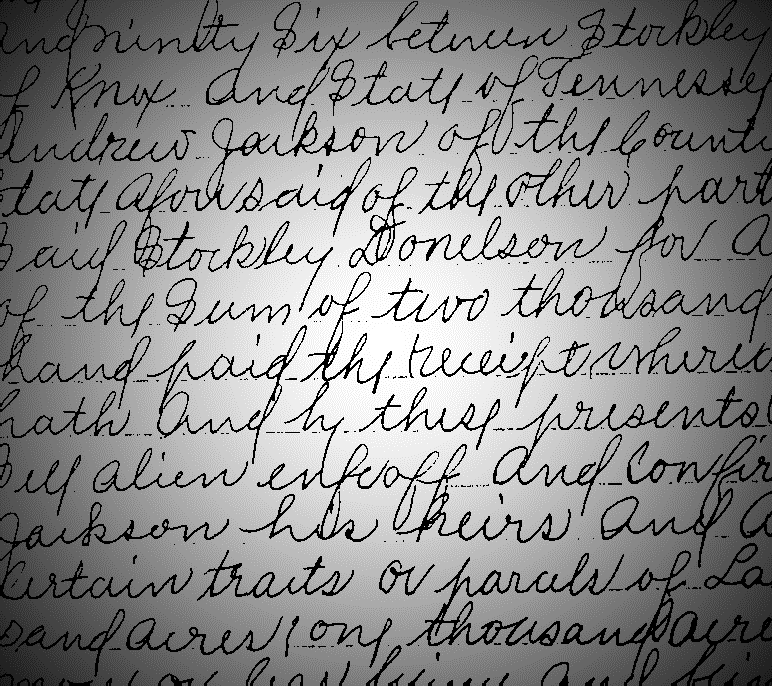
使用Otus最佳全局阈值的效果:
使用移动平均阈值: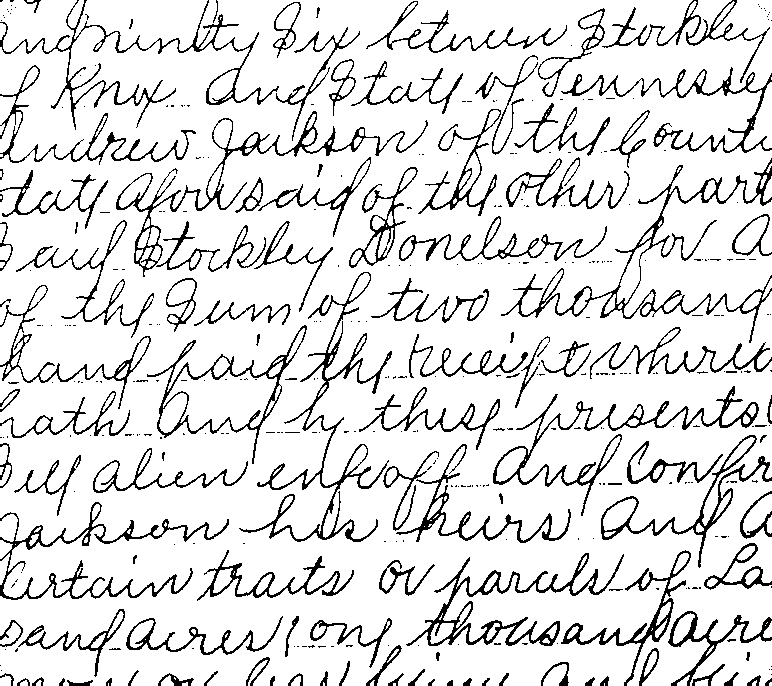
原图: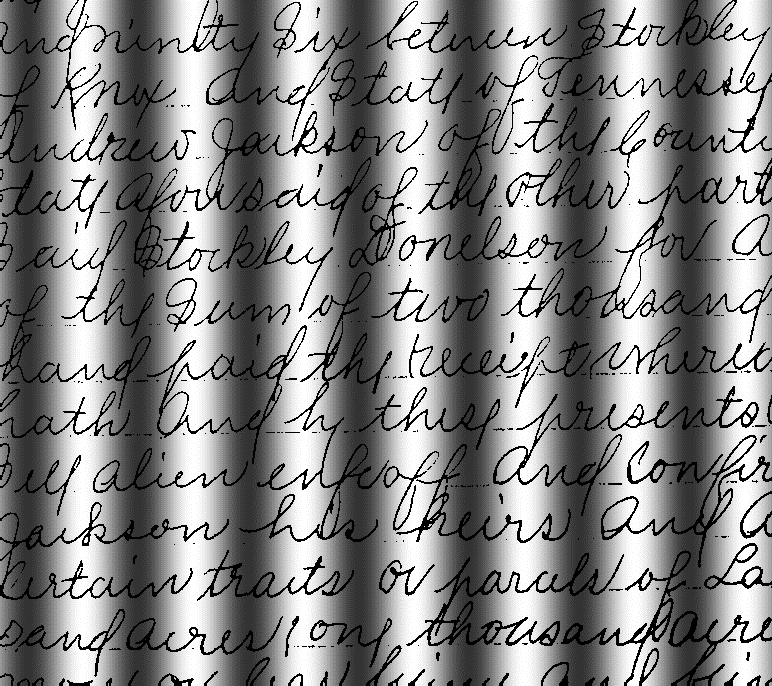
使用Otus最佳全局阈值的效果:
使用移动平均阈值: