数字图像处理——图像恢复

之前我们介绍了图像增强，图像增强是根据我们的需求对原始图像进行处理，如blur等。图像恢复则像是图像增强的逆，但是也不绝对，主要是我们希望回复图片真实原始的样子。比如deblur，去噪等等。这个待处理的图像不一定是我们增强的结果，也可能是硬件或者拍摄时候引入的噪声，模糊，抖动等等。

下面是几个distortion的例子：

上述中的blur分为optical blur（例如聚焦失败），以及motion blur（因为移动产生的模糊），而移动模糊又分为了全局（相机移动产生的模糊）和局部（拍摄的物体产生了移动，而背景是清晰的）。由于在形成image时候出现的这些噪声，我们拍摄的照片与真实的照片总是有差距的。我们假设真实照片应该是$u(m,n)$，而拿到的照片是$v(m,n)$，那么图像恢复的目标是找到一个操作$H$： $$H[v(m,n) ] \approx u(m,n)$$ 为了衡量恢复得好坏，我们使用MSE： $$\text{MSE} = \frac{1}{N^2} \sum_ {m=0}^M\sum_ {n=0}^N [u(m,n) - H[v(m,n) ]]^2$$ 不过，需要知道的是这个只是在评测一个算法的时候利用实验的数据来做，因此噪声可能是人为模拟实际添加的，然后根据原来的图片与处理之后的图片进行对比。一般来说如果在这些图片上表现良好，现实中也会有不错的表现。毕竟实际上，我们无法得到真正的”True image”。

一般来说，我们假设图像的distortion由两部分组成：degradation与noise，模型如下：

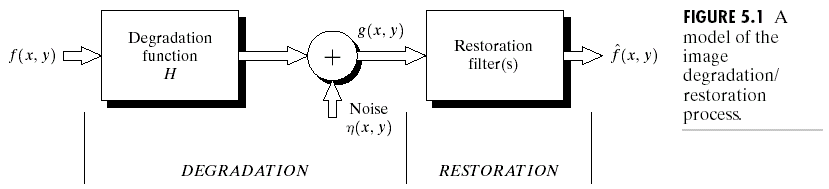
这里degradation一般是某种卷积操作，也就是： $$g(x,y) = h(x,y) * f(x,y) + n(x,y)$$ 对应到频域： $$G(u,v) = H(u,v)F(u,v)+N(u,v)$$ 那么想要做restoration，就是找一条返回去的路。

噪声

无从下手可以先从简单的开始。比如这里，我们先单独考虑噪声。一般来说噪声有下面几种：

Gaussian noise: $$p(z)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(z-\mu)^{2} }{2 \sigma^{2} } }$$ Rayleigh noise: $$p(z)=\left\{\begin{array}{ll}{\frac{2}{b}(z-a) e^{-\frac{(z-a)^{2} }{b} } } & {\text { for } z \geq a} \\ {0} & {\text { for } z< a}\end{array}\right. \mu=a+\sqrt{\frac{\pi b}{4} } \quad, \quad \sigma^{2}=\frac{b(4-\pi)}{4}$$ Erlang (Gamma) noise: $$p(z)=\left\{\begin{array}{ll}{\frac{a^{b} z^{b-1} }{(b-1) !} e^{-a z} } & {\text { for } z \geq 0} \\ {0} & {\text { for } z<0}\end{array}\right. \mu=\frac{b}{a} \quad, \quad \sigma^{2}=\frac{b}{a^{2} }$$ Exponential noise: $$p(z)=\left\{\begin{array}{ll}{a e^{-a z} } & {\text { for } z \geq 0} \\ {0} & {\text { for } z<0}\end{array}\right. \mu=\frac{1}{a} \quad, \quad \sigma^{2}=\frac{1}{a^{2} }$$ Uniform noise: $$p(z)=\left\{\begin{array}{ll}{\frac{1}{b-a} } & {\text { if } a \leq z \leq b} \\ {0} & {\text { otherwise } }\end{array}\right. \mu=\frac{a+b}{2} \quad, \quad \sigma^{2}=\frac{(b-a)^{2} }{12}$$ Impulse (Salt and Pepper) noise(椒盐噪声): $$p(z)=\left\{\begin{array}{ll}{P_ {a} } & {\text { for } z=a} \\ {P_ {b} } & {\text { for } z=b} \\ {0} & {\text { otherwise } }\end{array}\right.$$ 他们的图像分别如下：

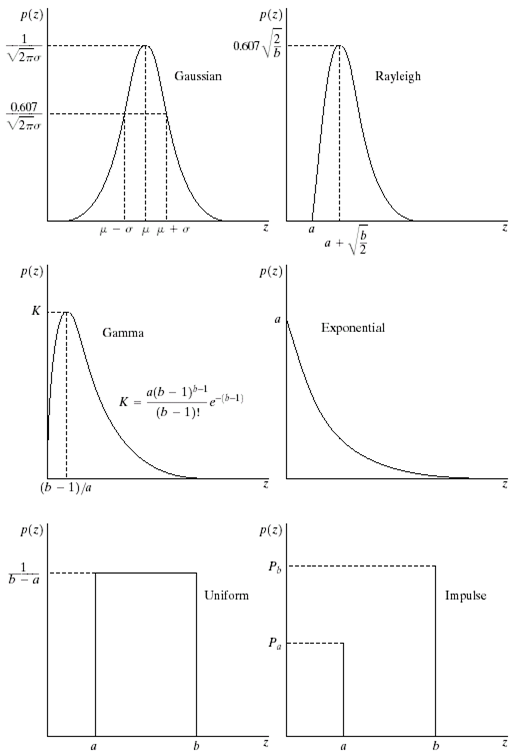
对于一张图片添加不同的噪声，可以得到下面的几种效果：

原图：

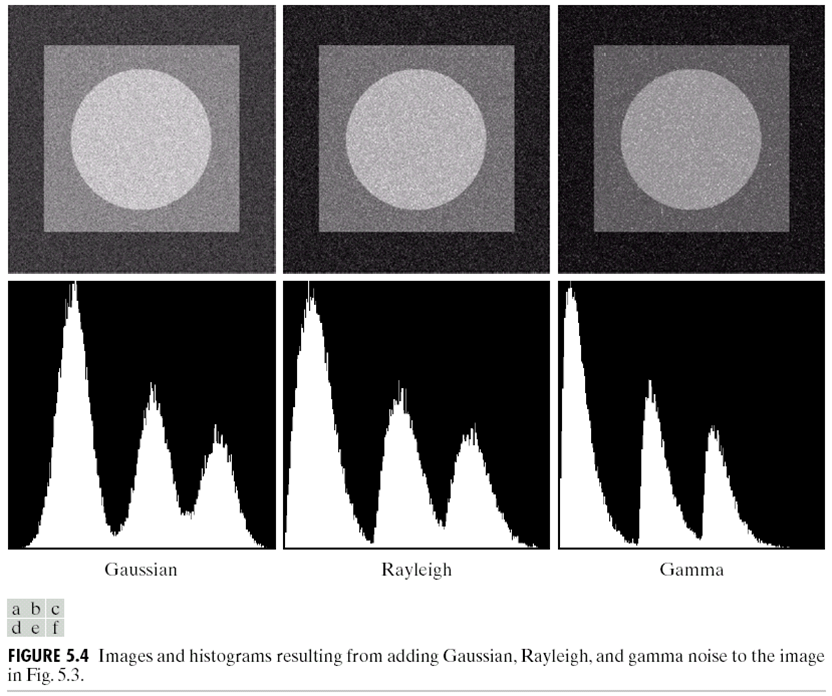
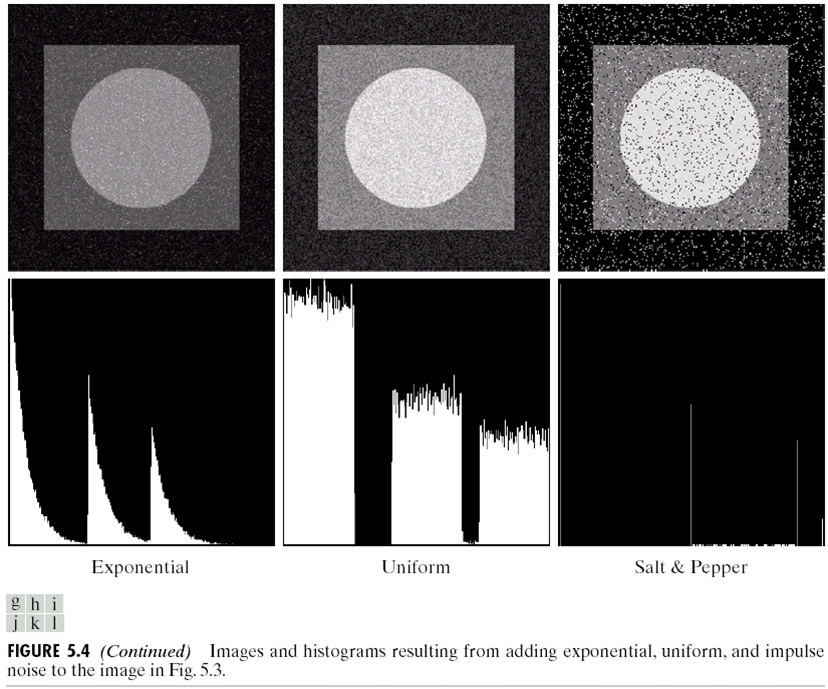
那么，如何知道图片$v(m,n)$上的噪声是什么类型？首先，选择一个图片应该比较平滑的区域，画出他的直方图。实际上，我们可以根据直方图的形状来估计噪声的类型，因为理论上平滑区域的直方图是只有一条线，因此直方图的形状实际上是噪声的形状，如下图：

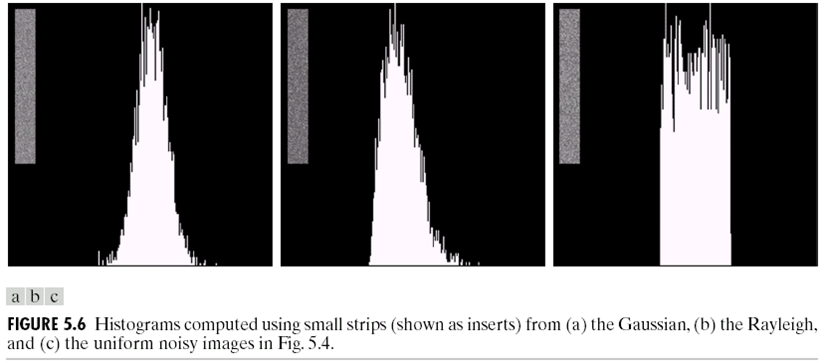
很明显，第一个应该是高斯噪声，而第二个是Rayleigh，第三个是uniform噪声。

如果我们只考虑噪声，那么这里的Degradation中的$H$就是一个单位矩阵，与$F$相乘后并不改变$F$的值，用公式表示如下： $$ g(x,y) = f(x,y) + n(x,y)\\ G(u,v) = F(u,v) + N(u,v) $$ 而根据直方图，我们可以估计出噪声的均值，方差等等，从而从源头上实现降噪。这个降噪的过程也就是使用滤波器。对于不同的噪声可以使用不同的滤波器来完成降噪。例如对于椒盐噪声可以使用中值滤波器，或者均值滤波器（会使得图像变得模糊）去除。除此之外我们还有最大最小值滤波，以及频域上带阻，带通等等滤波器。正如之前说的，对于带阻（通）滤波，可以有理想的，高斯的以及在理想与高斯之间的Blutterworth滤波：

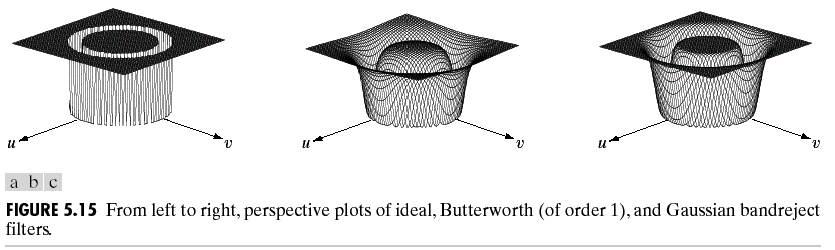
理想带阻滤波： $$H(u, v)=\left\{\begin{array}{ll}{1} & {\text { if } D(u, v)<D_ {0}-\frac{W}{2} } \\ {0} & {\text { if } D_ {0}-\frac{W}{2} \leq D(u, v) \leq D_ {0}+\frac{W}{2} } \\ {1} & {\text { if } D(u, v)>D_ {0}+\frac{W}{2} }\end{array}\right.$$ Blutterworth： $$H(u, v)=\frac{1}{1+\left[\frac{D(u, v) W}{D^{2}(u, v)-D_ {0}^{2} }\right]^{2 n} }$$ 高斯带阻滤波： $$H(u, v)=1-e^{-\frac{1}{2}\left[\frac{D^{2}(u, v)-D_ {0}^{2} }{D(u, v) W}\right]^{2} }$$ 下面是一个带阻滤波的例子：

在这里，再介绍一个Notch滤波。它转到空间域下的可视化如图：

数学形式： $$H(u, v)=\left\{\begin{array}{ll}{0} & {\text { if } D_ {1}(u, v) \leq D_ {0} \quad \text { or } \quad D_ {2}(u, v) \leq D_ {0} } \\ {1} & {\text { otherwise } }\end{array}\right.$$ 其中： $$\begin{array}{c}{D_ {1}(u, v)=\left[ \left(u-\frac{M}{2}-u_ {0}\right)^{2}+\left(v-\frac{N}{2}-v_ {0}\right)^{2}\right]^{\frac{1}{2} } } \\ {D_ {2}(u, v)=\left[ \left(u-\frac{M}{2}+u_ {0}\right)^{2}+\left(v-\frac{N}{2}+v_ {0}\right)^{2}\right]^{\frac{1}{2} } } \\ {H(u, v)=\frac{1}{1+\left[\frac{D_ {0}^{2} }{D_ {1}(u, v) D_ {2}(u, v)}\right]^{n} } } \\ {H(u, v)=1-e^{-\frac{1}{2}\left[\frac{D_ {1}(u, v) D_ {2}(u, v)}{D_ {0}^{2} }\right]^{n} } }\end{array}$$ 在频域上，它的图像如下：

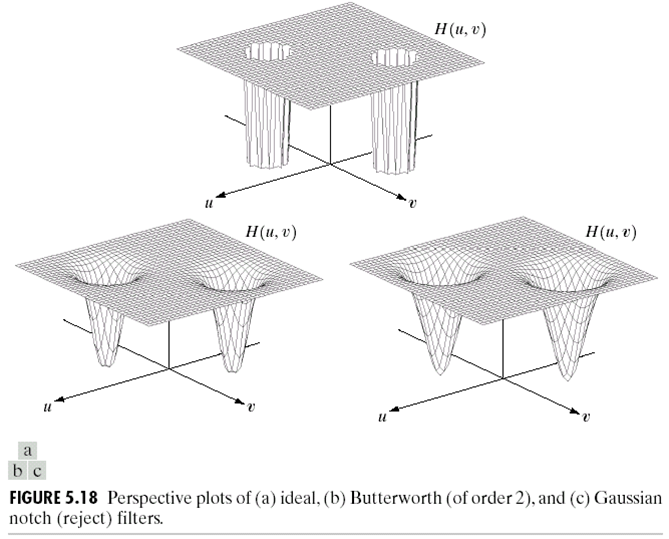
可以看到的是它阻塞了两个特定区域的频率，同样从sharp到smooth，也有理想的North滤波，Blutterworth North滤波，高斯Notch滤波。

线性，空间不变的Degradatioon

下面这张图，是一个经过高斯滤波，然后产生模糊的情况。

Blur操作，在频域上的表现是一个低通滤波器。假如我们已经知道了这里的$H$的形式，忽略噪声$N(u,v)$，那么对于原始图像$F(u,v)$的估计就是： $$\hat F(u,v) = \frac{G(u,v)}{H(u,v)}$$ 这个过程如下：

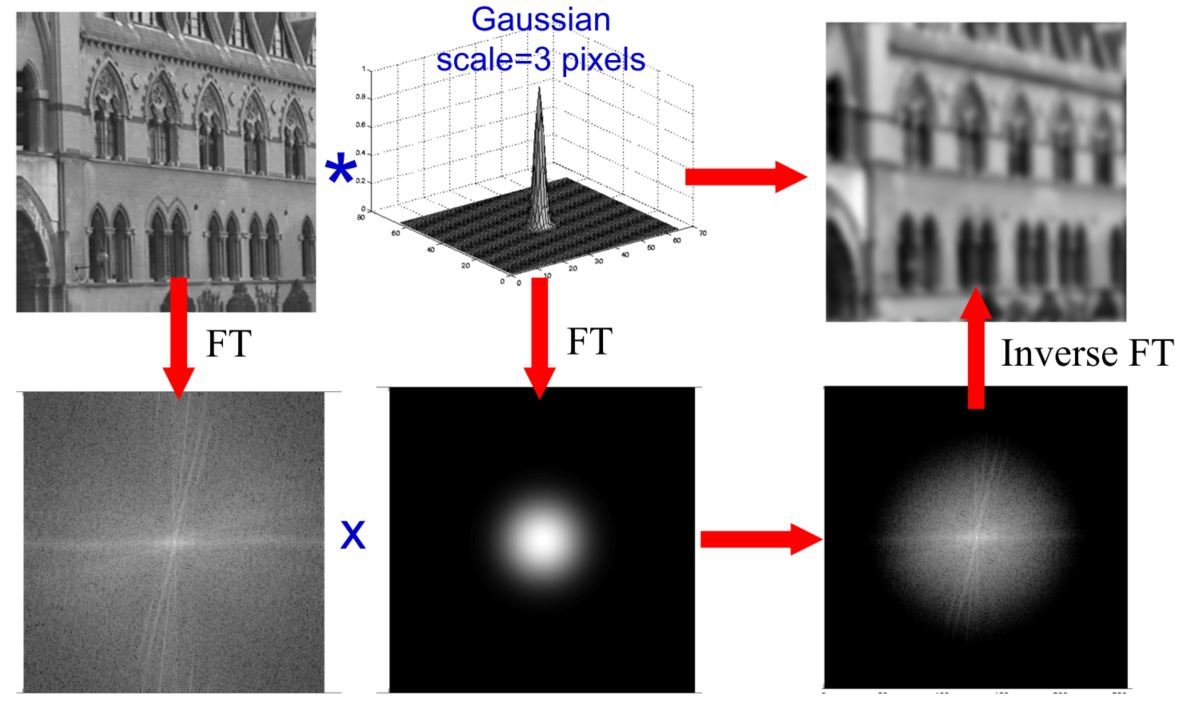
我们可以看看对于一张图片加上不同的高斯滤波之后产生blur，然后反向来deblur的几个例子：

这几张图，原始图是一样的，而加上不同的高斯滤波后造成不同程度的模糊，可以看到模糊程度越高，而deblur的效果越差。Why？

原因主要是因为我们忽略了这张图片本身具有不可避免的噪声（由于硬件传感器等造成的），而deblur则会放大这个噪声的效果。 $$ G(u,v) = H(u,v)F(u,v) + N(u,v)\\ \hat F(u,v) = G(u,v)/H(u,v) = F(u,v) + N(u,v)/H(u,v) $$ 这个过程用一个直观的解释如下：

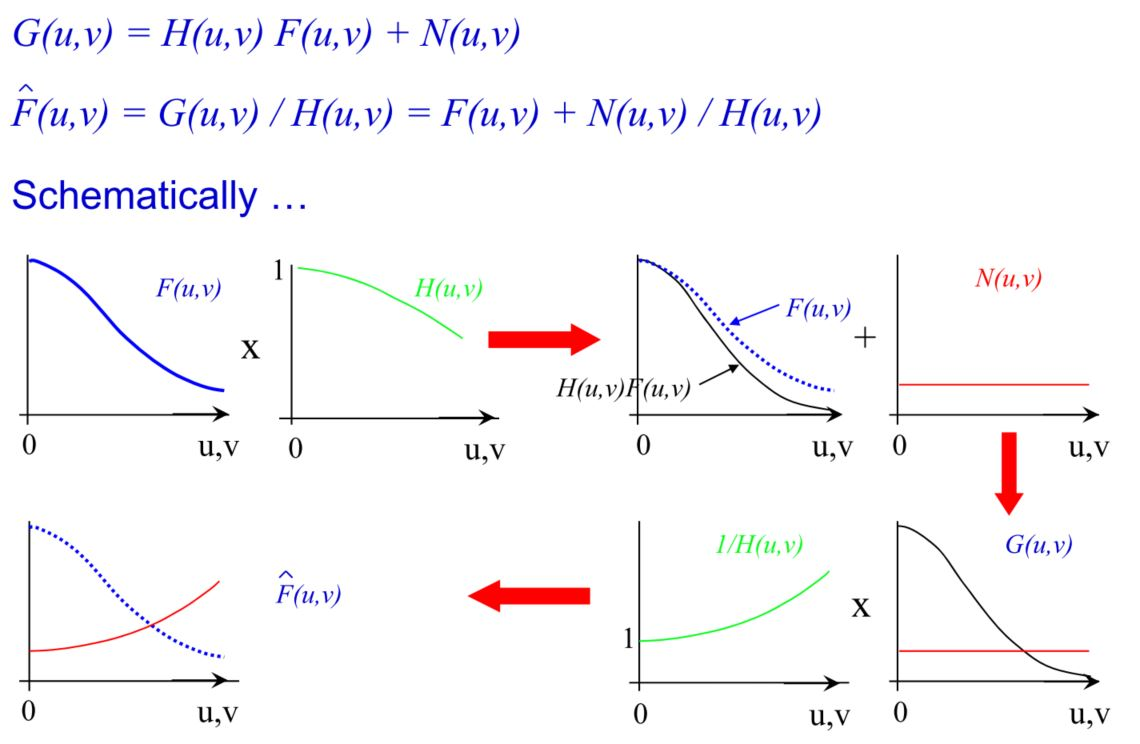
因此诞生了一个新的Wiener滤波器： $$ \hat F(u,v) = G(u,v)W(u,v),\\ W(u,v) = \frac{H^*(u,v)}{\vert H(u,v) \vert^2 + K(u,v)} $$ 这里的$K(u,v) = frac{\vert F(u,v) \vert ^2}{\vert N(u,v) \vert ^2}$。而$F(u,v)$以及$N(u,v)$可以大约估计得到，或者$K$由经验确定一个常量。Wiener Filter在最小化MSE： $$\sum_ {x,y}(f(x,y) - \hat f(x,y))^2$$

这其中的推导可以去查阅相关的论文。关于它的直观化理解如下：

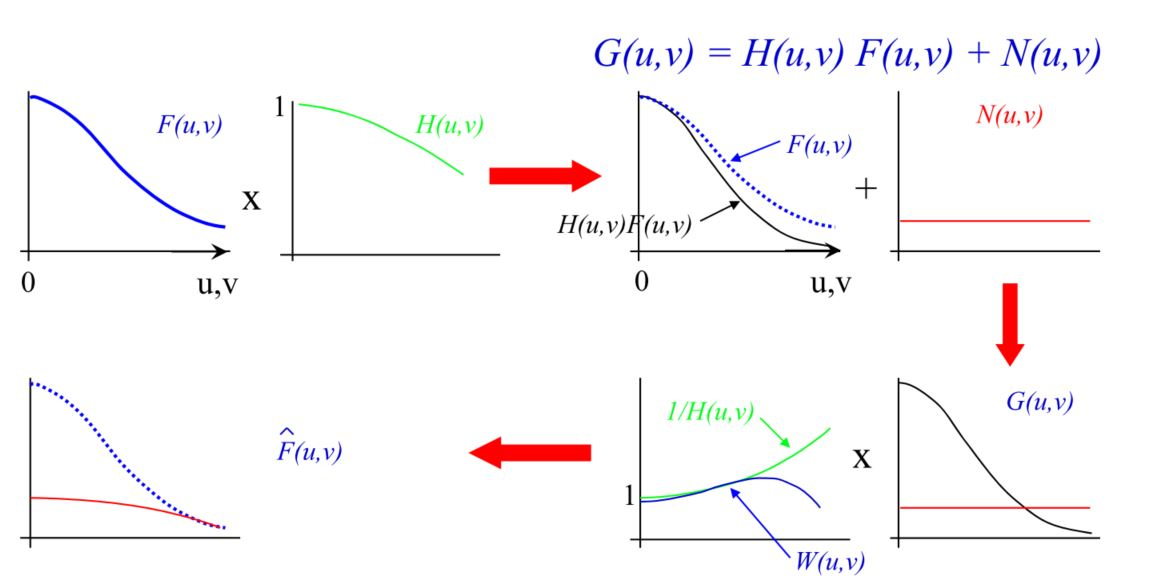
可以看到，$W(u,v)$的形状到了高频之后形状并不会持续的上升，而会有下降，这样一定程度上即保证了高频区域的恢复也保证了不会放大噪声。

它的deblur效果如下(这里的高斯滤波$\sigma = 1.5\text{ pixel}$,noise $\sigma = 0.3\text{ gray level}$ )：

因此可以看到，了解噪声产生过程是非常重要的，可以帮助我们处理更高的一些算法。

要注意这里的高斯噪声，和高斯滤波，二者是不同的，第一种是噪声分布是高斯分布，然后直接叠加到像素，而第二种是卷积操作，在频域上的乘积，造成图像的模糊。因此他们的处理方法也是不同的，对于高斯噪声的处理一般采用自适应滤波。

实际上，关于Deblur有非常多相关的研究。这里有一篇关于夜间图片deblur的文章。夜晚的blur造成主要是因为深夜因为光照不足，所以需要更长的曝光时间，而人的手上细微的抖动就会被叠加出现模糊。而夜晚图片经常会有点光源，这些光源的轨迹实际上就代表了相机运动的轨迹，文章就以这个为先验信息，来进行deblur，这是一个非常新奇的观点：
Deblurring Saturated Night Image With Function-Form Kernel。