数字图像处理——空间域滤波
上次介绍了图像增强的算法,而这次介绍一些滤波的内容。滤波是图像处理中非常重要的一部分内容,而且它涉及到很多的算法,我们需要合理选择,来达到自己的目的。
滤波算法分为空间域上的和频域上的。这一部分,我们主要介绍空间域上的滤波。
实际上,空间域的滤波,也就对应的之前提到的块操作。一般来说,空间域上的滤波又叫邻域操作算子。它会根据周围的像素,决定中间像素的值。我们定义块的大小($3\times 3$,或者$5\times 5$或其他),然后对Block中的各个像素分配权重,做卷积操作(convolution)或者相关操作(correlation)。而根据目的不同,如何定义权重以及块的大小,以及卷积或者相关操作,可以演化出很多不同的算法。
对于滤波操作,可以用下面的数学形式来表述:
$$
f(x, y) \longrightarrow[w(x, y)] \longrightarrow g(x, y)
$$
而从$f$到$g$的转换,除了需要权重$w$,还需要的是卷积或者相关操作。其中相关定义如下:
$$
w(x,y) \star f(x,y) = \frac{1}{\sum_ {i,j} w(i,j)}\sum_ {i=-a}^{a}\sum_ {i=-b}^bw(i,j)f(x+i,y+j)
$$
而卷积定义如下:
$$
w(x,y)*f(x,y) = \frac{1}{\sum_ {i,j} w(i,j)} \sum_ {i=-a}^{a}\sum_ {i=-b}^bw(i,j)f(x-i,y-j)
$$
卷积和相关的定义区别只是卷积在计算时会对滤波器旋转180°。如果滤波器是中心对称的,那么它的卷积操作和相关操作是一致的。对于图像边缘的,由于没有办法构成一个block,那么可以重复边缘的像素,或者是从图像另一端获取像素,或者直接忽略即可。而滤波的过程,可以看做是权重向量和块向量的乘积,非常简单。
使用上述卷积相关操作的滤波有,均匀滤波,各个权重为1。可以想象,这样的滤波会让这个图像变得非常平滑模糊,但是它对于一些噪声的去除是非常有用的。高斯滤波,也就是对最中间像素的值会有最高的权重,块中其余像素的权重是按照二维高斯分布决定的,这样的滤波能减少模糊,保留一定的细节。高斯函数:
$$
h(x,y) = e^{-\frac{x^2 +y^2}{2\sigma^2} }
$$
对于$5 \times 5$滤波器,标准正态高斯滤波如下:
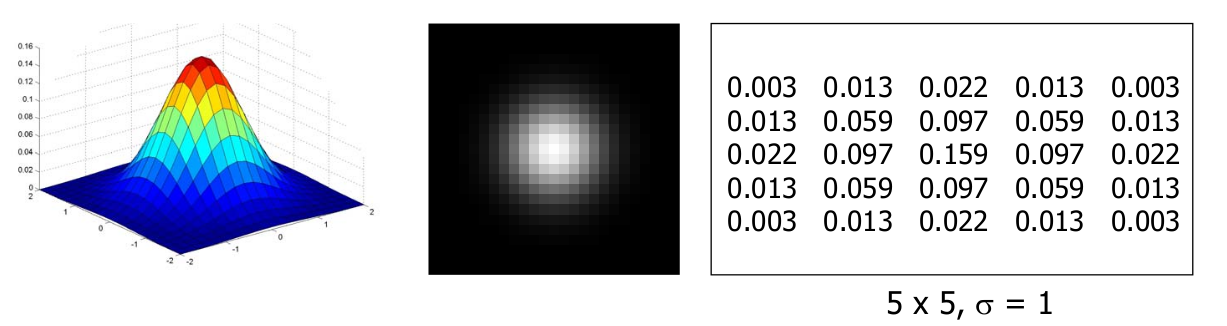
除了使用上述方法,进行卷积或者相关操作的线性运算,我们还有例如中值滤波,最大值滤波最小值滤波等等。也就是,在block中,选取中位数,最大值,或者最小值作为中心点的像素。其中,中值滤波有时候也有比较好的去噪效果,尤其是椒盐噪声和斑点噪声。
下图为中值滤波去除椒盐噪声: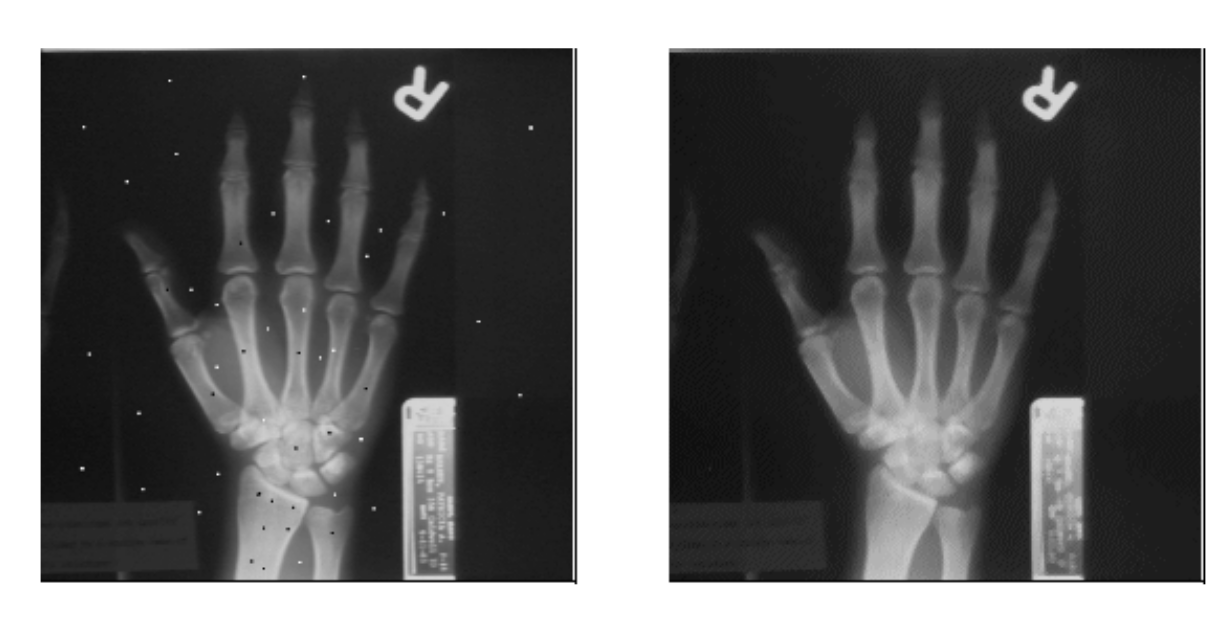
边界增强
图像滤波有一个重要的作用是提取边界。对于边界,一个简单的想法是边界两侧像素值相差很多。在数学角度上,描述两侧差距大小也就是变化率,而梯度很符合这个概念。
离散函数的导数退化成了差分,一维一阶差分公式和二阶差分公式分别为:
$$
\frac{\partial f}{\partial x} = f(x+1) - f(x)\ \frac{\partial ^2 f}{\partial x^2} = f(x+1) +f(x-1) - 2f(x)
$$
我们先从简单的入手,也就是图像的偏导数。我们可以计算横向的和纵向的边缘,以及45度的,对于这些计算,有多种算子,但是实际上本质就是左右(或者上下)像素相减,求某个方向上的偏导数,只是对于不同位置的偏导权重不同,下面分布是Sobel,Kirsch以及Robinson算子:
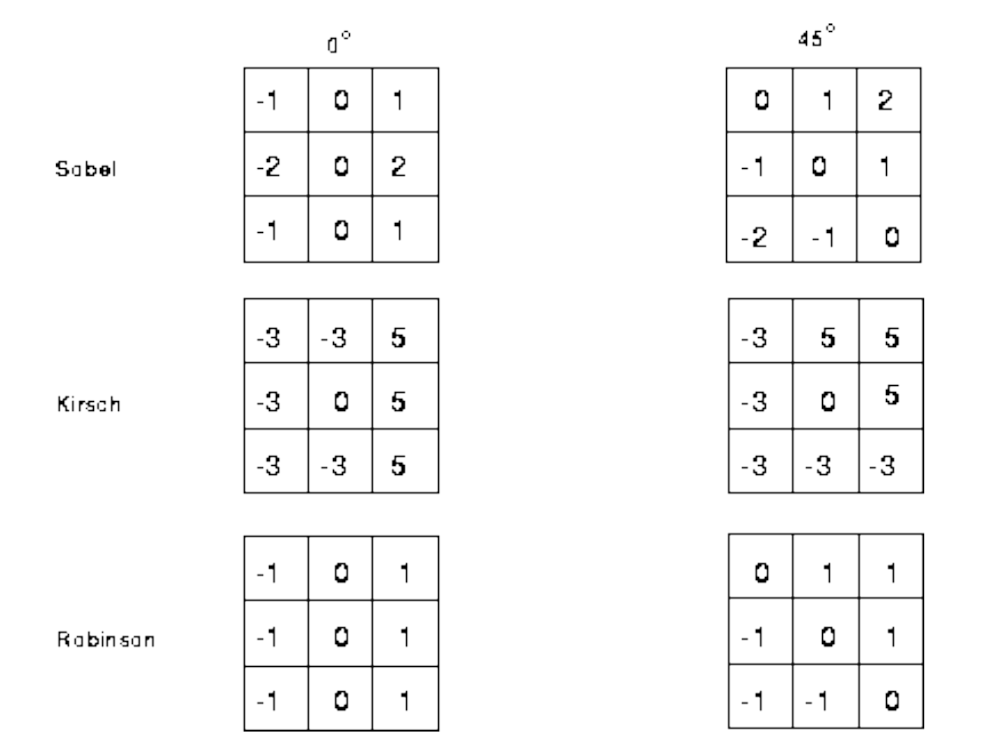
上面的内容都非常简单,因为是简单的一阶偏导。而另一方面,如果上升到二阶导数,我们这里介绍拉普拉斯算子。
$$
\text{Laplacian: }L(x,y) = \frac{\partial ^2 I}{\partial x^2} + \frac{\partial ^2 I}{\partial y^2}
$$
由之前提到的二阶导数,我们可以得到拉普拉斯算子的在图像上的差分形式:
$$
\nabla^2 f(x,y ) = f(x+1,y) + f(x-1,y) +f(x,y-1)+f(x,y+1) - 4f(x,y)
$$
写成filter mask如下:

可以看到它的形式是非常简单的。而拉普拉斯算子对噪声很敏感,因此使用之前需要降噪,或者直接高斯拉普拉斯算子(Laplacian of Gaussian):
$$
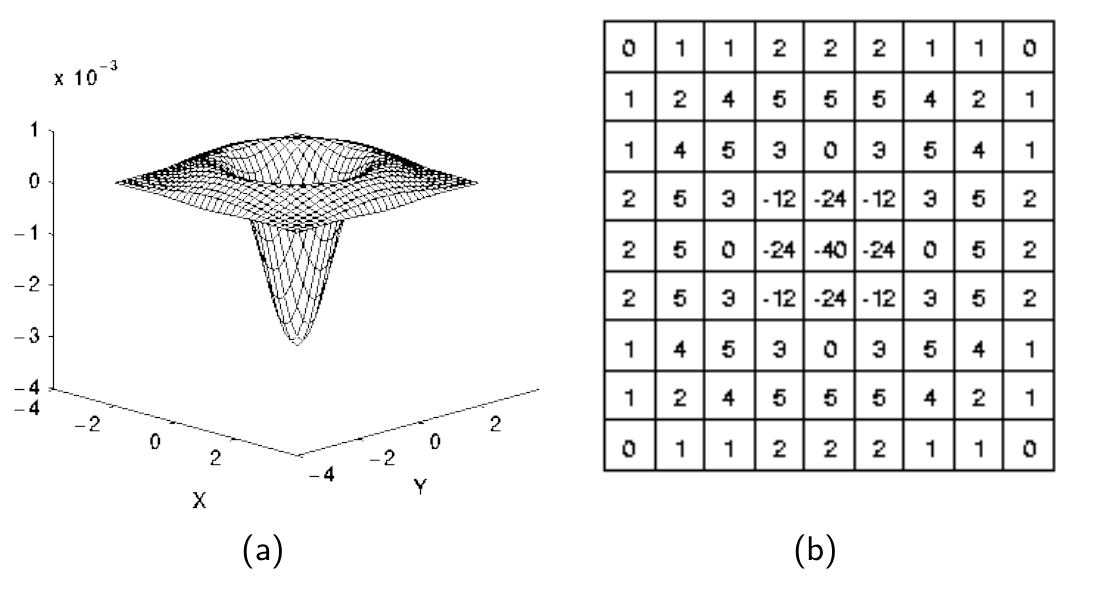
\operatorname{LoG}(x, y)=-\frac{1}{\pi \sigma^{4} }\left[1-\frac{x^{2}+y^{2} }{2 \sigma^{2} }\right] e^{-\frac{x^{2}+y^{2} }{2 \sigma^{2} } }
$$
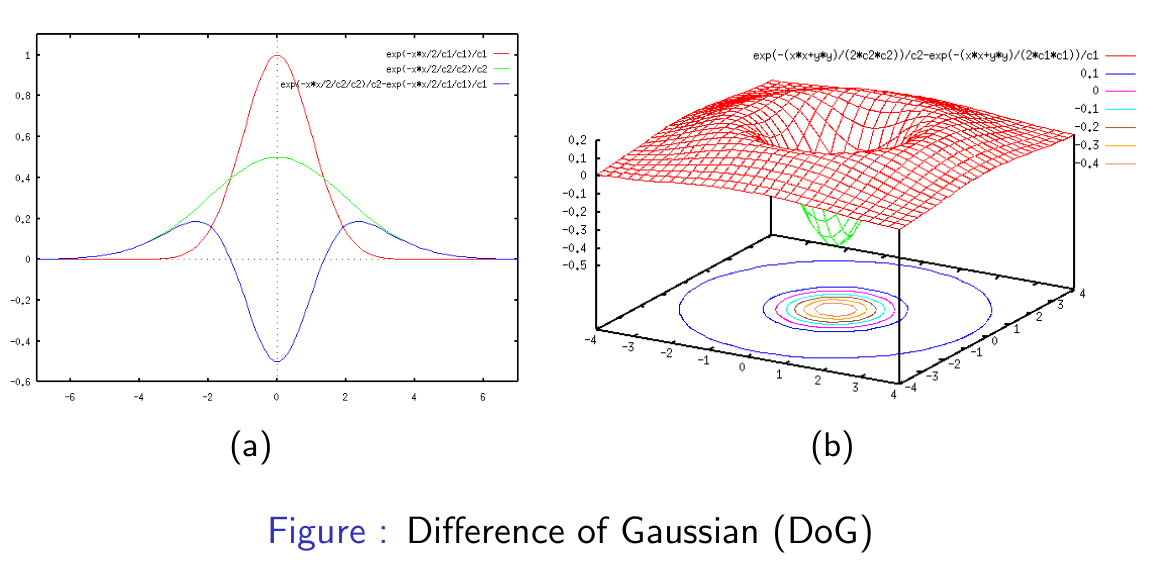
另外,也可以使用高斯差分(Difference of Gaussian):
$$
D o G \triangleq G_ {\sigma_ {1} }-G_ {\sigma_ {2} }=\frac{1}{\sqrt{2 \pi} }\left[\frac{1}{\sigma_ {1} } e^{-\left(x^{2}+y^{2}\right) / 2 \sigma_ {1}^{2} }-\frac{1}{\sigma_ {2} } e^{-\left(x^{2}+y^{2}\right) / 2 \sigma_ {2}^{2} }\right]
$$
锐化
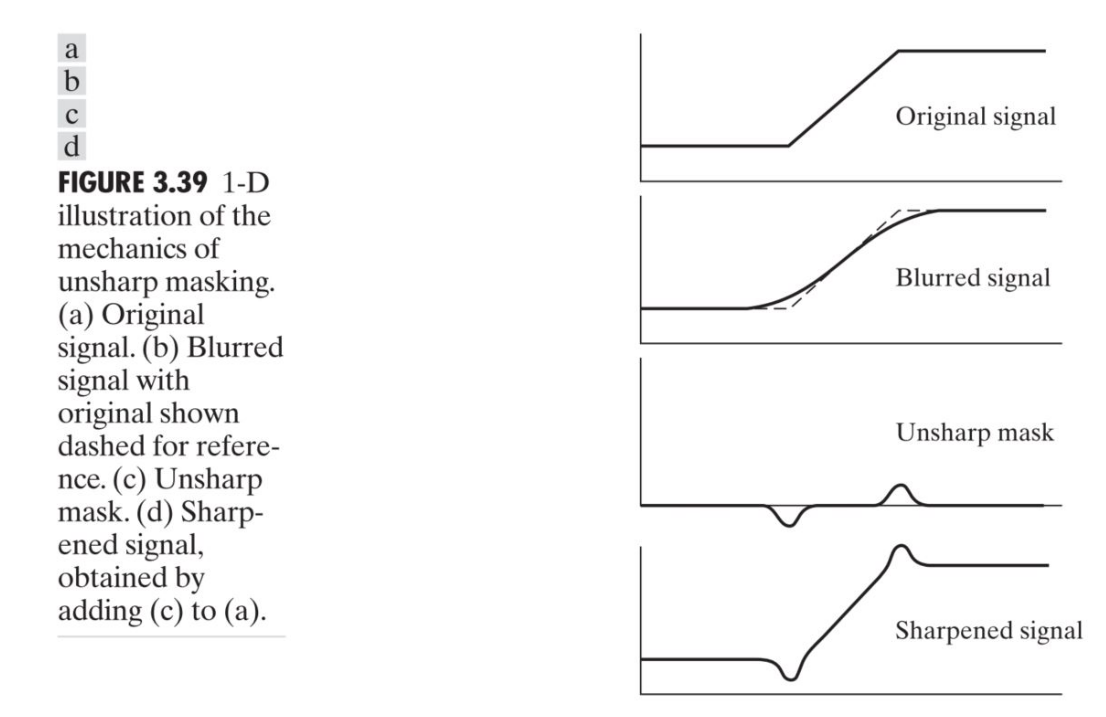
有时候我们希望锐化图片边缘。对于锐化,主要做的是进一步加大有差异像素之间的差异。一个普遍的做法是:
- 模糊原来的图像,使用均值滤波等
- 用原来的图像,减去滤波后的图像,得到的就是差异值
- 将这个差异值叠加到原来的图片上
用数学描述如下:
$$
g_ {mask}(x,y) = f(x,y) - \overline f(x,y);\ g(x,y) =f(x,y) + k \cdot g_ {mask}(x,y),k\ge 0
$$
当$k \ge 1$时候,上述算法被称为高通量滤波(highboost filtering)。

这里有一个关于边探测的阅读材料:
supplemental material
我想在这里再终点说明一下其中的一个边探测算法:Canny Edge Detection。Canny边探测算法可能是计算机图形学中使用最多的边探测算法。
Canny提出了边检测算法的3个衡量准则:
- 低错误率,尽可能减少漏检和误检
- 最优定位,检测到的边缘应该在实际边缘的中心,因为比如使用高斯拉普拉斯算法,得到的会是模糊后的边缘,因此边缘很粗,这样并不利于确定实际的边缘在哪
- 在图像中任意边缘应该只被标记一次,图像噪声不应产生伪边缘
Canny算法步骤如下:
- 高斯模糊
- 计算梯度的幅度和方向,可以使用上面介绍的sobel等算子
$$
\begin{array}{l}{\left(S_ {x}, S_ {y}\right) \text { Gradient Vector } } \ {\text { magnitude }=\sqrt{\left(S_ {x}^{2}+S_ {y}^{2}\right)} } \ {\text { direction }=\theta=\tan ^{-1} \frac{S_ {y} }{S_ {x} } }\end{array}
$$


3. 进行非极大值抑制。因为进行模糊后,边缘检测的结果往往比较粗,进行非极大值抑制可以有效减少这个现象,而非极大值抑制需要使用梯度的方向和幅度。非极大值抑制如下:因为一般的边缘是个曲线,我们通过2得到了曲线的梯度,比较梯度方向(正向和反向)的值,如果当前值(幅度)为最大,则保留,否则抑制,也就是设为0,从而细化边界。

4. 双阈值。一般边缘检测算法只有一个阈值,而Canny边缘检测有两个阈值,比大的阈值大称为强边缘,比大的阈值小,但是比小的阈值大称为弱边缘,而删除掉比小的阈值更小的点。
5. 滞后边界跟踪。这个是Canny算法和其他的算法差别最大的地方。Canny算法假设强边缘检测点一定是边缘点,而弱的边缘检测点则有可能是边缘点,也有可能是噪声。而通常来说,边缘是连通的,而噪声却不会,因此滞后边界跟踪会检查递归检查连通的弱边缘点的8连通领域像素,只要有强边缘点存在,这个条边就被保留下。也就是,我们检查一条弱边缘点构成的边,通过搜索弱边缘点的8连通领域像素,来得到连通的边缘点,只要这些边缘点中有强边缘点,就留下这条边。

下面是Canny算法的效果:
