图形学——计算机动画
阴影是图形学中显示真实感图像非常重要的一部分。我们在画画时候也知道,简单的话加上了一点阴影效果会大大增加,仿佛瞬间一幅画变得立体。这篇文章简单介绍一下图形学中的阴影部分。
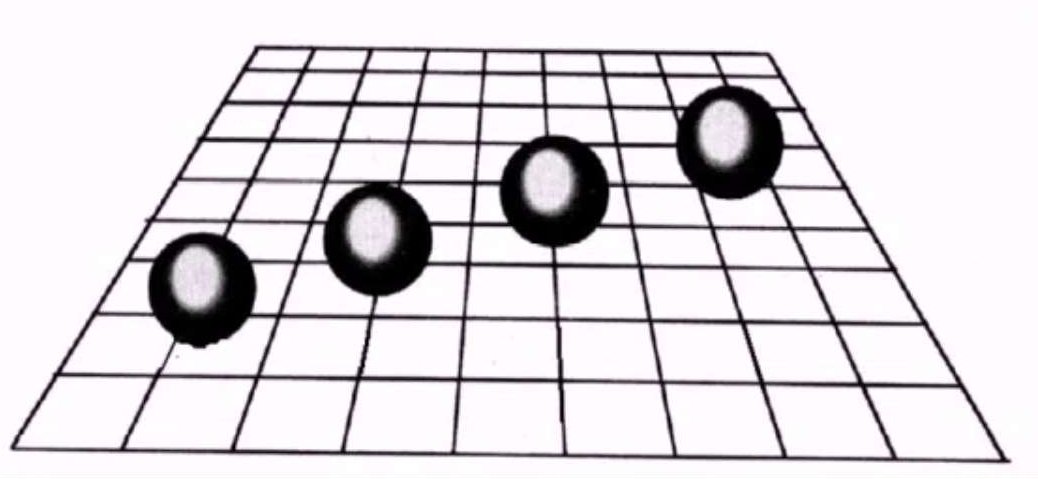
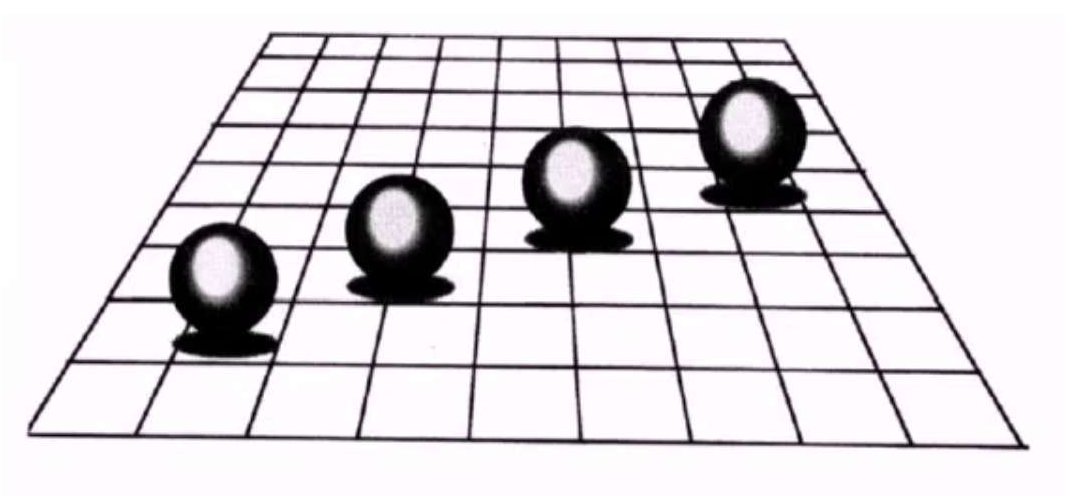
阴影不光可以给模型增加真实感,而且也是模型位置的重要信息,如下图,除掉阴影部分小球在视觉投影上的位置是一样的,但是画出阴影后我们就可以明白小球具体的位置,不同的阴影对应着不同的位置。因此阴影给物体的位置提供了非常重要的视觉提示。

阴影的定义
考虑一个光源L照明的场景,场景中每个物体作为接受者都可能被光源照到,如果有一点P不能看到光源的任何一部分,它被称为本影,如果从P点可以看到光源的一部分,那么它被称为半影,如果P可以看到光源的全部,那么它不在阴影区内。本影和半影统称为阴影。
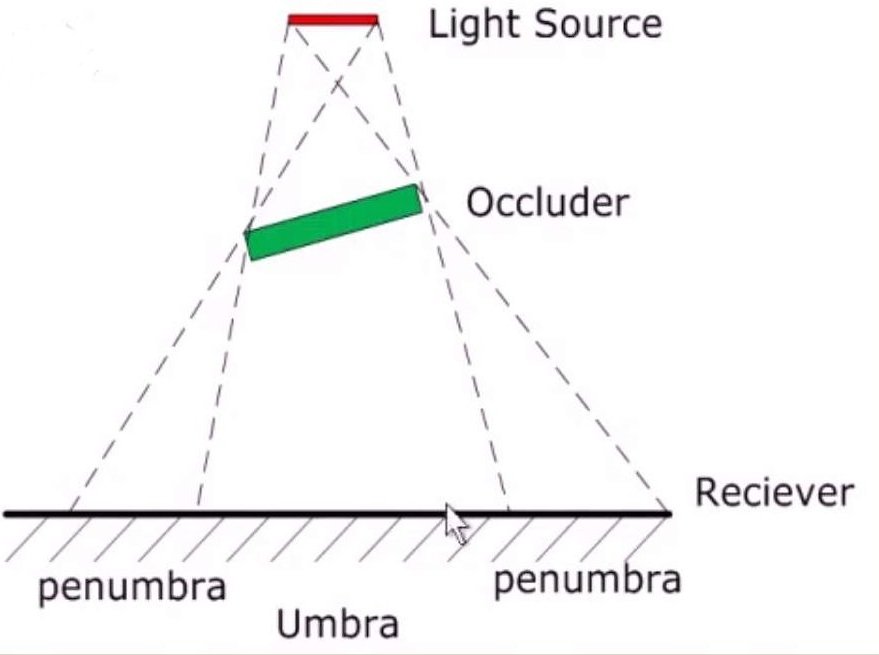
如果光源是理想的点光源,那么就只有非阴影区域和全影,而不存在半影,但是在实际中并不存在理想的点光源。
一般来说阴影有以下几个类型:
- 附着阴影:接受者的法向背离光源的方向
- 投射阴影:接受者的法向朝着光源方向,但是光源被遮挡物所遮挡
- 自阴影:接受者和遮挡物是属于同一物体,比如一个狼牙棒上的阴影
在图形学中,根据处理阴影的办法,又可以分两种:
- 硬阴影。通常将阴影理解为一个二值状态,一个点要么在阴影区内,要么不在。也就是考虑光源都是点光源,只有全影和非阴影区域的区别(或者及时不是点光源,也不区分半影和全影)。在现实中,硬阴影是很难见到的,即使是太阳也会有很大的角展,产生的不是硬阴影。但是点光源在计算机上更容易模拟,对硬阴影的计算有很多实时的算法。
- 软阴影,就是会考虑到半影和全影的区别,对某个点可以看到光源部分的多少来决定某个点的明暗程度。软阴影更真实,不过在有限展度的光源(通常是面光源)下,确定本影和半影区域通常比较困难,这意味着需要求解3D空间中的可见关系,这是个非常困难的问题。
下图是硬阴影和软阴影的区别:
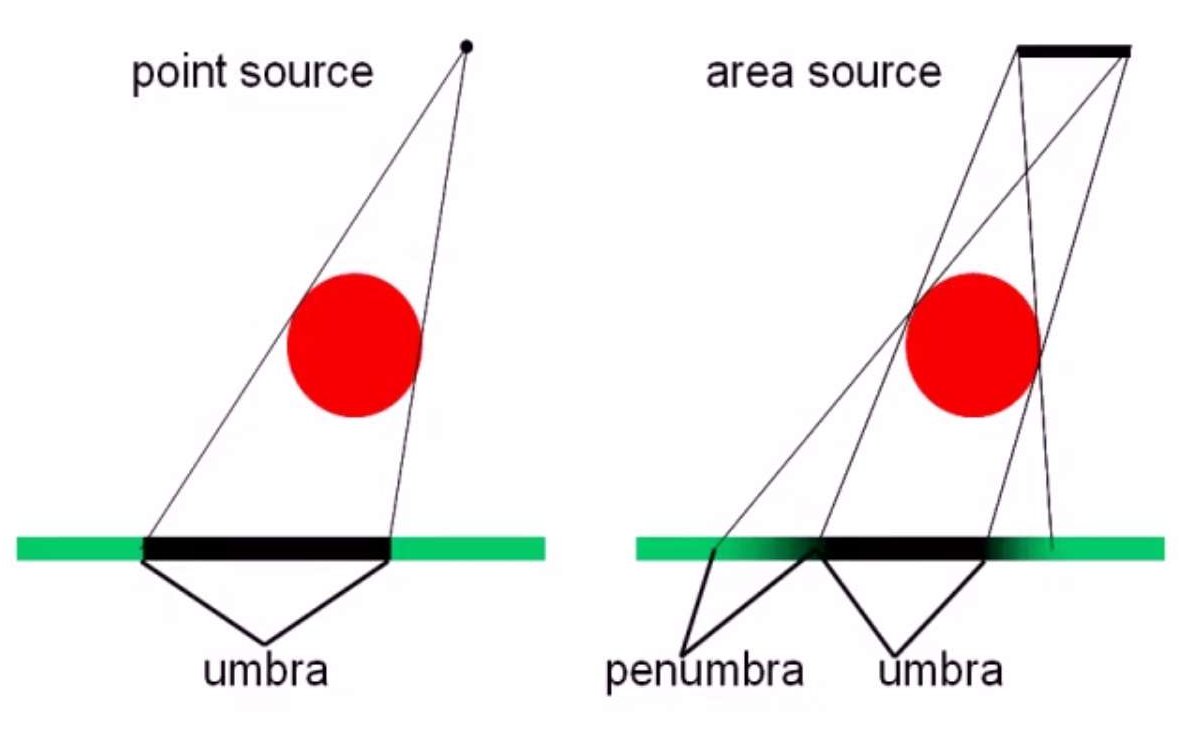

很明显,软阴影有更好的真实感。
平面阴影
计算阴影最基本的方法就是将遮挡物表面的点投影到出现有阴影的物体表面。如果物体表面是平面,则被称为平面阴影。平面阴影相对来说更容易计算。对于平面的阴影计算,只需要简单利用投影矩阵就可以。考虑下面的例子,我们需要计算的阴影位于$y=0$平面上,光源坐标为$l=(l_x,l_y,l_z)$,现在我们想求得$p$点$x,z$坐标,如下图:
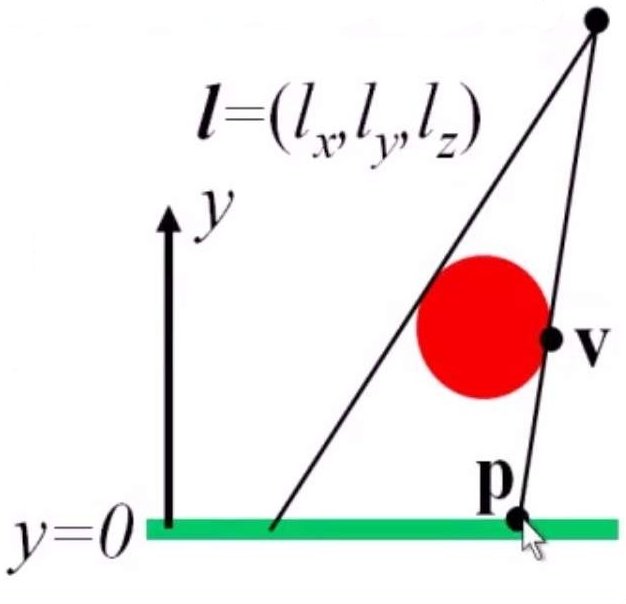
根据相似三角形可以得到:
$$
\frac{l_y}{l_y - v_y} = \frac{l_x - p_x}{l_x - v_x}
$$
则:
$$
p_x =\frac{l_yv_x - l_xv_y}{l_y - v_y}
$$
我们也可以根据同样的道理计算出来:
$$
p_z = \frac{l_yv_z - l_z - v_y}{l_y - v_y}
$$
这两个方程可以用一个投影矩阵$M$来表示:
$$
M = \begin{bmatrix} l_y & -l_z & 0 & 0\ 0&0&0&0\ 0&-l_z&l_y&0\ 0&-1&0&l_y \end{bmatrix}
$$
通常来说,这个平面是任意的,一般的平面方程为:
$$
n\cdot p + d = 0
$$
类似于$y=0$的情况,可以计算出对应的投影矩阵:
$$
M = \begin{bmatrix} n\cdot l + d - l_xn_x & -lxn_y & -l_xn_z & -l_x d \ -l_yn_x & n \cdot l + d - l_yn_y & -l_yn_z & - l_yd\ -l_zn_x & -l_zn_y & n \cdot l +d - l_zn_z & -l_zd\ -n_x & -n_y & -n_z & n\cdot l \end{bmatrix}
$$
求阴影点位置时:$Mv = p$,$v$是遮挡物上的点。
绘制平面投影很简单,对投影处的点使用暗色并进行去光照绘制即可。投影算法的局限性在于只能做平面阴影。
曲面上的阴影
对于曲面上的阴影,简单的使用投影矩阵就不可行了。
有一个非常聪明的做法是将阴影图像作为纹理贴到物体表面。这种方法被称为阴影纹理。我们可以将光源作为视点,绘制处这个视角下的图像,白色背景,但是遮挡物画成黑色。得到的图像作为纹理图,然后对遮挡物后的曲面进行纹理映射。纹理映射上一篇内容介绍了,以此实现绘制阴影的效果。

这个方法的不足是依然不能绘制自阴影。
下面介绍两个比较重要的阴影生成算法,它们分别是阴影域(shadow volume)算法和阴影图(shadow map)算法。
阴影域
阴影域算法(有时候也称体阴影)由Crow提出,可以将阴影投射到任何物体表面。它的思想是,首先,想想三维空间中一个点和一个三角形,连接点和三角形三个顶点并延长们可以得到一个衍生的无穷远三棱锥,如下图:
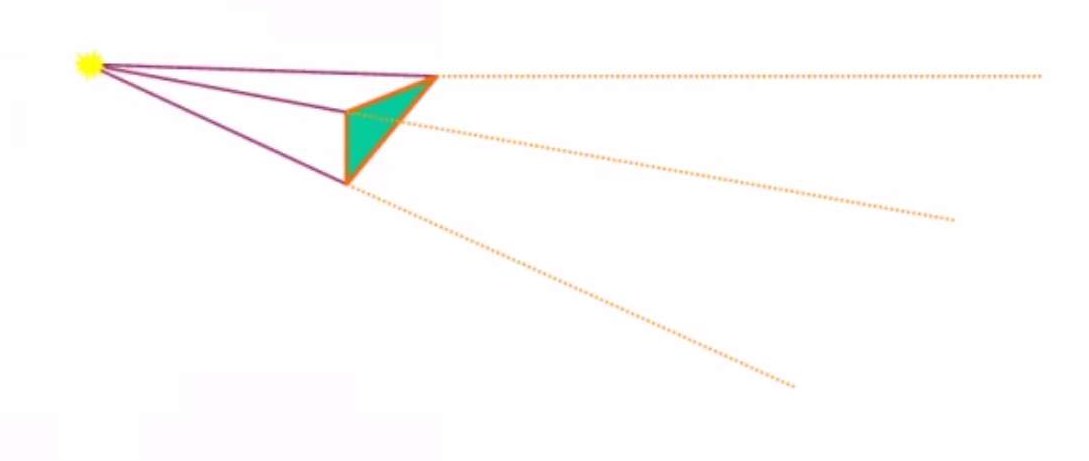
三棱锥部分去掉顶端以外的区域就在阴影内,被称为阴影域。
在绘制中,我们从视点向屏幕的某个像素投射了一条射线,该射线与场景中的某一物体交于一点,因此我们需要确定该点是否位于阴影中,也就是确定它是否位于阴影域中。Crow提出一个非常聪明的做法,假设视点位于阴影域外,维护一个计数器,初值是0。某个像素投出的射线每次进入到一个阴影域中,计数器+1,每次出一个阴影域,计数器-1,最后当射线达到交点的时候,我们只要确定计时器是否大于0。如果计数器大于0,则该点位于阴影内部。
从几何上实现上面的算法(需要多次求交)并不容易,因此在实现上述算法时,Crow使用了模板缓存(Stencil Buffer),对每一个像素存储一个计数值。
- 算法最开始,清空所有的模板缓存,然后将整个场景绘制到帧缓存中,只是用环境光分量和发光分量,并获取对应的颜色信息以及深度信息(z-buffer)。
- 接着,绘制所有阴影域的正面(面向光源的面),如果一个像素的深度值(正面到视点平面的距离)小于之前算好的深度值(z-buffer),那么对该像素对应的模板缓存计数+1。
- 绘制所有阴影域的反面,如果一个像素的深度值小于之前的深度信息(z-buffer),则对该像素对应的模板缓存计数-1。
- 根据模板缓存对所有像素再次绘制,只对模板缓存是0的像素绘制漫反射和高光分量,以此实现阴影效果。
下图是效果图:
阴影域算法有下面几个优点:
- 它不是基于图像的,因此不会局限于图像的分辨率,采样,质量等问题。任何情况下都可以生成很清晰的阴影。
- 上面的操作是可以高速并行的,因为各个像素是互相不影响的,可以使用通用的图形学硬件实现,仅仅需要一个模板缓存。
不过即使如此,阴影域算法依然不够块。因为阴影域算法需要求阴影域,场景中如果有较多的遮挡物,就会有很多的阴影域。他们会影响到性能。
阴影图
阴影图算法是Williams提出的,也是基于深度信息z-buffer的。它的思想是将点光源作为视点,求得深度图,被称为阴影图。

求对真正的视点穿过各个像素得到的射线与物体的交点,这个交点在光源求得的阴影图上有个对应的像素,比较该像素存储的深度值和交点的深度值的大小,如果交点深度值更大,则交点在阴影区内。说起来有点复杂,看图的话非常容易明白:
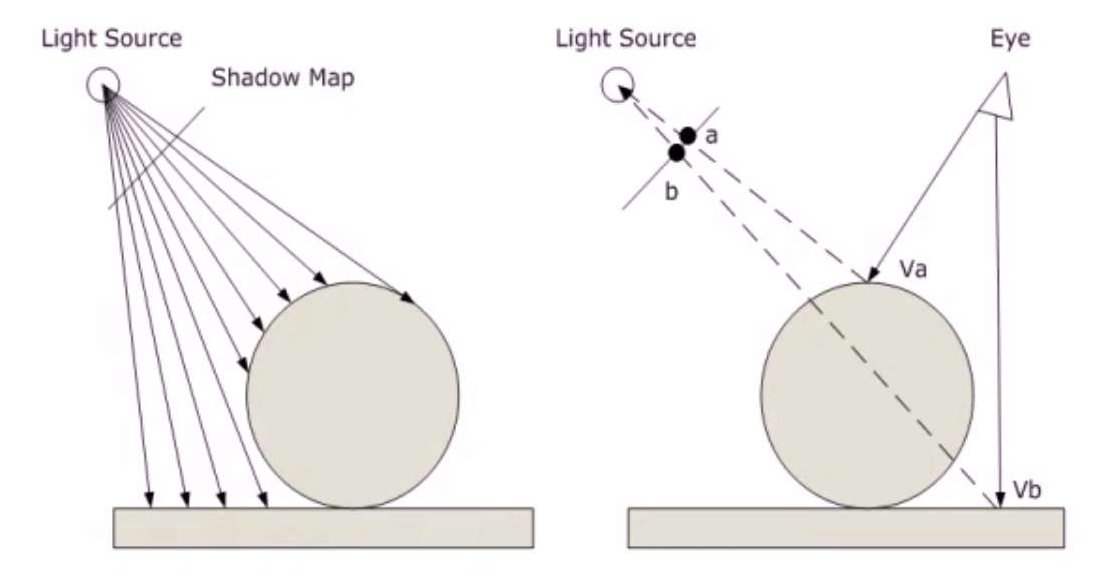
阴影图算法思想简单,而且运行高效。但是因为它是基于图像的,因此可能收到图像质量的影响。而且比较的时候,由于数值处理,很难达到完全相等的情况,需要设定一个范围$\epsilon$,在范围内就认为是相等的。而$\epsilon$的设置也会影响到结果。下面是阴影图算法求得的结果:

当$\epsilon$设得过小,可能会产生类似于下图的莫尔干涉条纹:

当$\epsilon$设得过大,又会使得阴影形状发生变形:

这两种阴影明显生成的都是硬阴影。在这两种阴影算法的基础上,还有很多变种,想了解更多的可以去查阅更多资料。