图形学——纹理
想要让模型逼真,对每个细节都进行刻画是一个很费力不讨好的办法。而使用纹理,模型还是原来的模型,进行贴图后就会变得非常逼真。这一篇文章会简单介绍一下纹理的相关内容。
纹理是用真实或者生成的图像贴到生成的三维模型上,将纹理应用于物体表面的过程被称为纹理映射。现纹理解决了两个问题:
- 通过纹理图片标识表面,用户不必建模几何细节
- 通过渲染简单的多边形模型和纹理,可以使得渲染过程更加高效
下面是几个应用纹理的例子:

下面3张图片分别代表了原始图片,二维纹理和三维纹理(几何纹理):



为了使用纹理,我们通常需要三个步骤:纹理采集,可以通过手工绘制,图片采集,过程纹理(程序生成),纹理合成等等;第二个是纹理贴图,用来将纹理的坐标与三维模型坐标建立映射;第三个是纹理滤波,因为直接将纹理映射后,可能还会产生一些人为痕迹,这时候需要对纹理进行采样滤波。
纹理采集
这里主要介绍过程纹理(Procedure)和纹理合成()。
过程纹理
过程纹理通过编写特殊的程序模拟物理形成过程或者材质外观,来合成纹理。例如大理石或者木头等一些特定的模式,可以通过非常简单的函数来模拟。不过过程纹理只适用于一些特定的纹理,对于一个没有已知程序代码的材质,无法通过该方法来合成。
最著名的过程式合成方法为:柏林噪声,下面是柏林噪声生成的纹理的例子:

在介绍柏林噪声之前,先说明一下什么是白噪声。白噪声是一种在所有频率处具有均衡能量密度的信号,因此白噪声的傅里叶变换是近似平坦的。它可以通过均匀的随机函数产生,比如产生一个二维的白噪声函数,可以用$[0,1]$区间的均匀分布随机函数产生的值作为每个像素的颜色。
柏林噪声与白噪声不同,它是一个有限频宽函数,可以通过对不同频带的白噪声求和得到:
$$
perlin = \sum_ {i=0}^{n-1}\text{interpolate}(white_i) \times p^i
$$
上式中,$n$是频带总数目,$p$是持久性,$i$是频带编号,其中$i=0$代表了最低频带。第$i$个频带的白噪声是一个简单的具有特定大小($2^i$)的白噪声。由于不同频带对应不同的图像大小,在求和前需要进行插值(不是很明白)。而持久性是一个用户指定的参数,通过它可以简单控制不同频带之间的相互权重,这个参数范围通常为$[0,1]$。
下图是一个柏林噪声的例子(左侧为柏林噪声,右侧为各个频带的白噪声):

实际上柏林噪声的算法还是比较复杂的,可以用来模拟很多真实场景,比如火焰,手绘,以及随机地图的生成等等。具体参考文章:improving noise。
基于柏林噪声,可以利用适当的过程生成丰富多样的纹理,比如大理石和木材,对应公式如下:
$$
\text{marble} = \cos(x + perlin(x,y,z))\
\text{wood} = g - \text{int}(g), \text{where } g = perlin(x,y,z) \times scale\
$$
纹理合成
纹理合成是只从一个特定的样本合成一个新的纹理。这种方法对用户更友好,只需要用户提供一个图像样本。而且由于图形学长期以来有很多研究致力于纹理分析,这方面也有很多实用的算法。
纹理合成技术可以被分为两类:基于像素的纹理合成和基于块的纹理合成。
Pixel Based
主要思想是逐像素地合成新的纹理,其中每个像素的值由局部邻域来确定(如$3\times 3, 5 \times 5$)。选择输入像素中具有最相思邻域的那个。如下图:
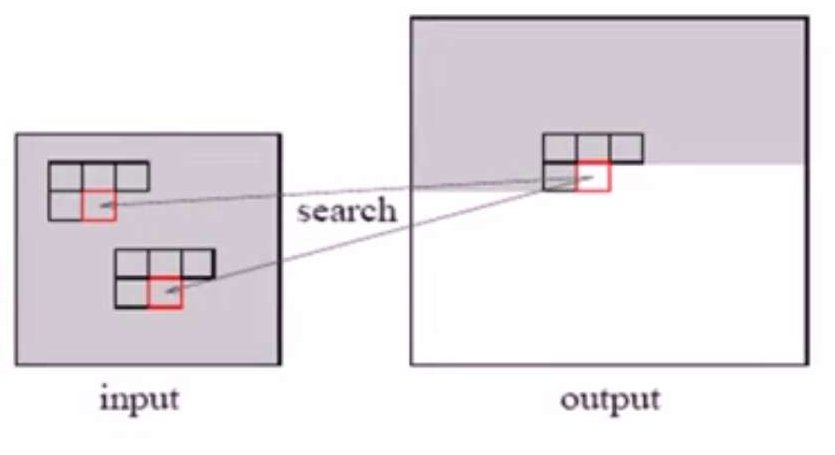
下面是一个基于像素的纹理合成结果:
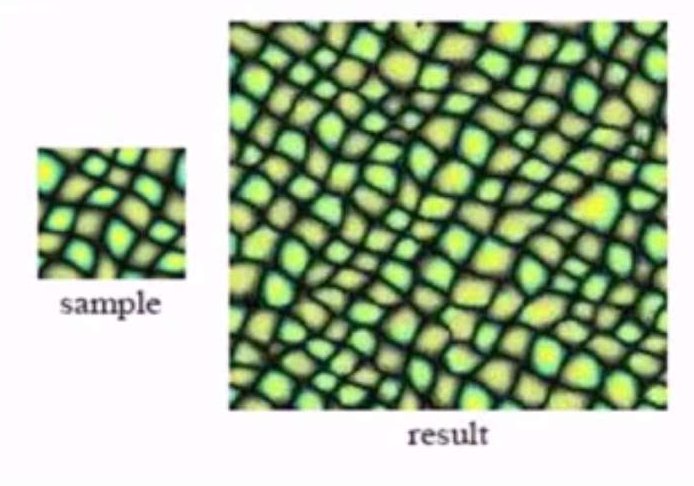
Block Based
基于像素的方法可以通过合成区块来改进。最重要的方法之一是Graph-cut,是目前效果最好的基于块的像素合成。想要了解更多可以查看:Graphcut Textures: Image and Video Synthesis Using Graph Cuts。
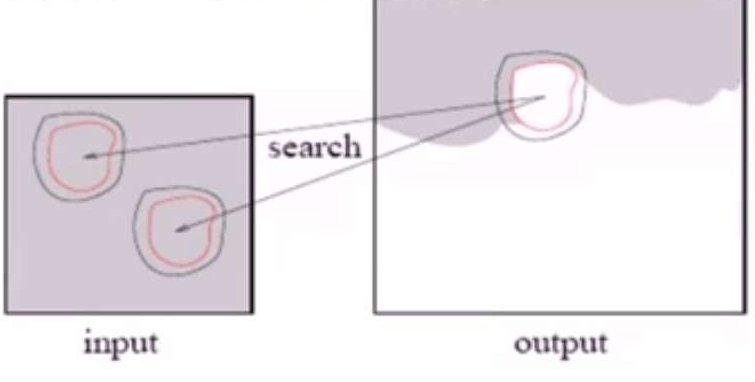
下面是一些Graph-Cut算法的结果:

纹理映射
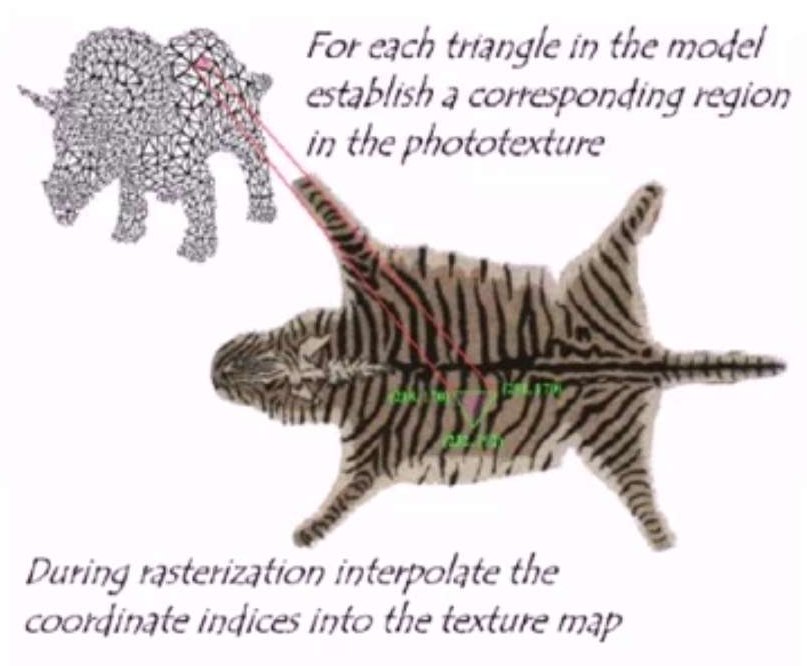
纹理映射,指的是给定一个模型和二维纹理图像,将图像映射到模型上。映射过程为,通过将模型点映射到$(u,v)$图像坐标方程来完成,这个方程被称为表面映射函数。
再给模型点着色时,我们根据表面映射函数从2维纹理中寻找适当的像素,并用该点去影响最终的颜色。如下图:
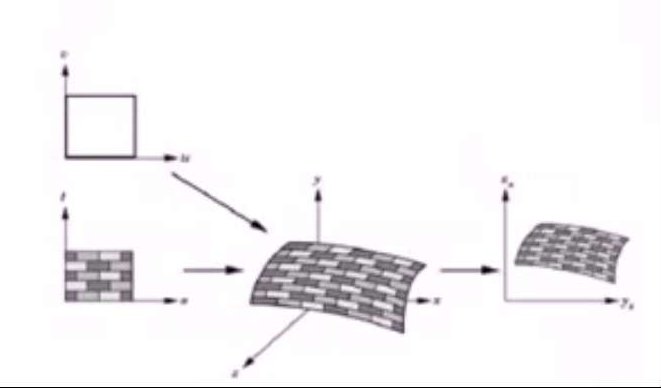
对于规则物体,如球体,立方体和圆柱体等等,我们可以通过自然参数化来得到表面映射函数,二对于非规则的复杂物体,有时候可能需要手工制定纹理坐标,为每一个顶点指定一个纹理坐标。
- 自然参数化。自然参数化示意图:
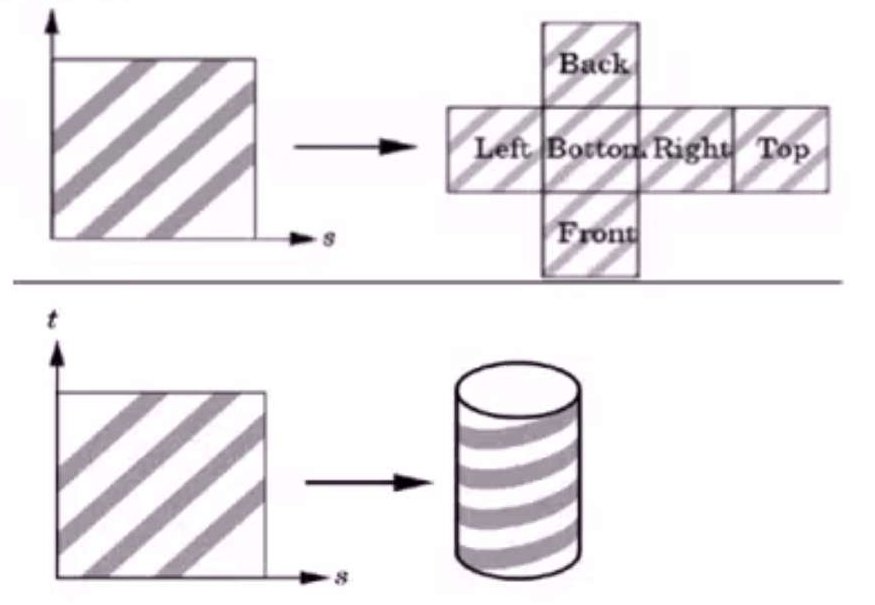
对于球体,可以采用球面坐标:(\theta, \phi) = (\pi u,2\pi v);
对于圆柱,可以采用圆柱坐标:(u,\theta) = (u,2\pi v).
- 手工指定纹理坐标,指给每个顶点指定一个纹理坐标,或者将图像空间中的一个三角形映射到物体空间。
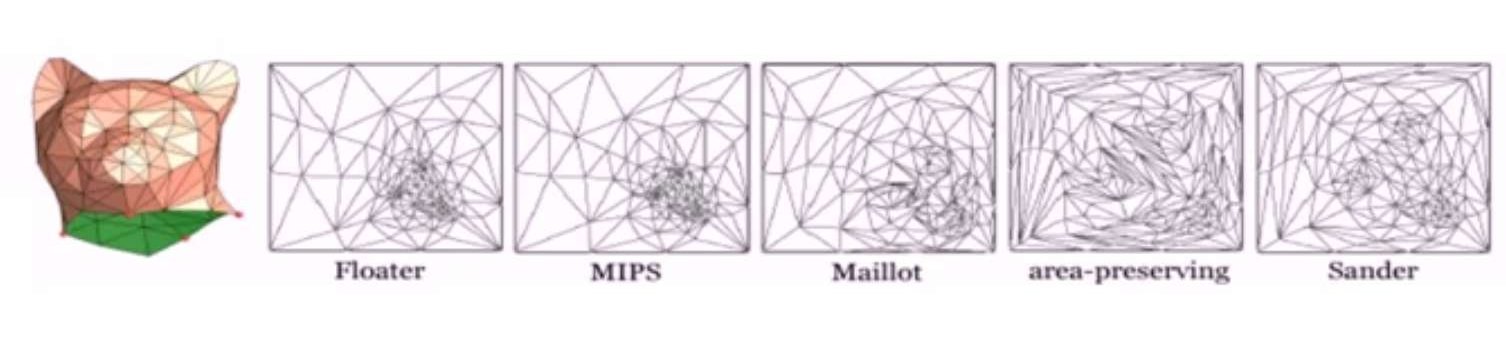
- 网格参数化。构造一个从三维模型到平面域的映射,如下图是几个不同算法的结果:
- 共形参数化与面积保持:反曲率映射。在网格上从网格边的边长到网格顶点的高斯曲率的映射称之为曲率映射,利用共性几何理论,由网格曲面的曲率映射的切映射,可以证明这个映射是可逆的。

上图的格子很不均匀,可以通过迭代达到均匀的结果:

具体算法需要更多资料。
纹理滤波
纹理映射之后,如果直接渲染,就有可能产生人为痕迹(artifacts),这些人为痕迹由信号走样(signal aliasing)引起。
走样和反走样
通常情况下,走样是由于信号采样频率过低产生,导致信号的很多高频特征的丢失,如下图:
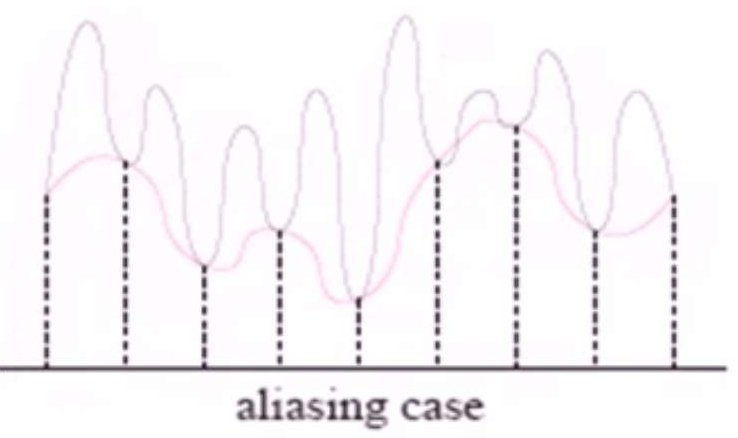
要解决这个问题,被称为反走样。一个方法是提高采样率。然而这个方法并不是总是可行。另外一个可行的方法是预先对信号进行滤波,得到一个更低频率的信号。
滤波一般分为两种:各项同性和各项异性。
各向同性(Isotropic)
材质转换是一种各向同性算法,构造由一组经过预滤波和重采样图像构成的图像金字塔。这些图像是原图在$\frac 1 2, \frac 1 4, \frac 1 8$等尺度对应的采样。在光栅化的过程中,我们计算与期望采样率最近似的图像的序号。
各向异性(Anisotropic)
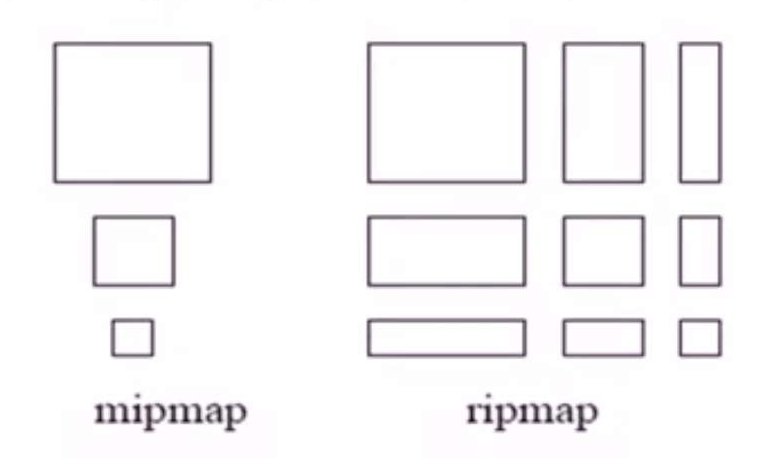
材质转换的问题是它有时候会带来模糊。我们可以通过计算各向异性滤波构造ripmap来代替mipmap(多级纹理),如下图:
下图是未进行滤波,各向同性与各项滤波的对比:

高级主题
最后我们聊一些纹理的高级主题。
体纹理
之前讨论的纹理都是表面纹理,只需要二维纹理图像。二体纹理,纹理值构成三维数组,也就是对模型内部也会进行纹理映射。下面是一个体纹理示意:

其他纹理
基本的纹理映射是给曲面赋予颜色,另外的,我们影响曲面的别的属性来进行纹理映射。如表面法向(凹凸贴图),几何(移位贴图),光源辉度(环境贴图)等。
凹凸贴图将纹理当成单通道的高度方程,由实际纹理图中的导数计算法向量。它并不改变表面实际形状,但是渲染的时候看上去形状却变了。
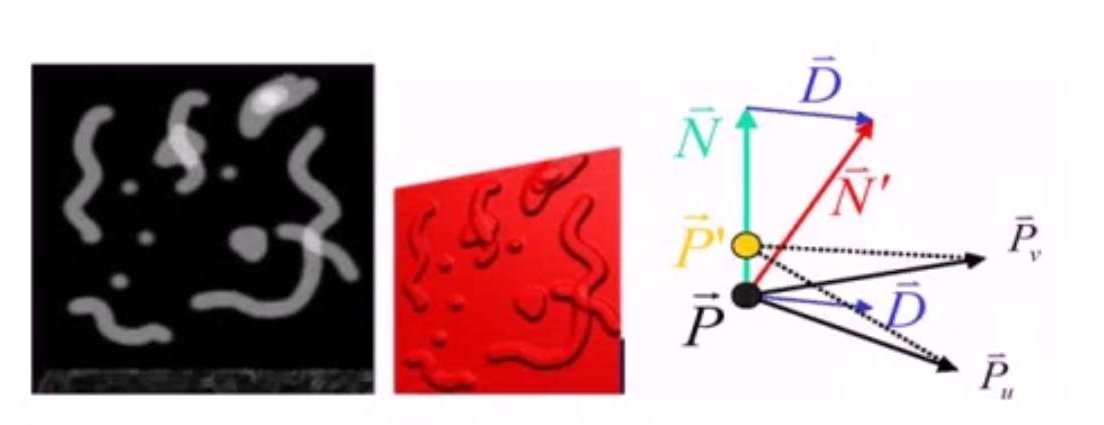
下面是凹凸纹理的两个例子:

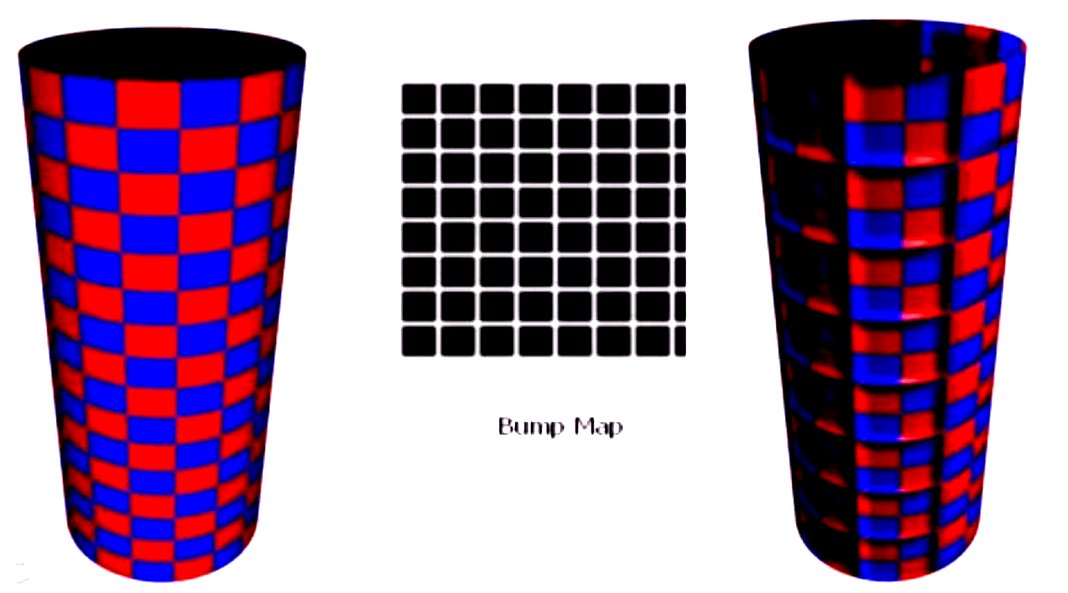
凹凸纹理不会产生侧面轮廓的效果,也就是虽然表面看上去是凹凸的,但是边缘依然很齐,这个和实际是不符的。而且它不支持自遮挡或者自阴影。
而移位贴图可以做好上面的限制,它利用纹理图真实的移动曲面点,在确定可见性之前,必须先对几何进行移位,它需要在预处理时进行,而不是硬件渲染时候进行,移位贴图效果如下:

本文只是对纹理各个方向有个粗略介绍,并没有涉及到讲解某个具体的算法,简直主要是show图片了。如果想要实现,需要更深入的了解。