图形学——Bezier曲线及曲面

在图形学中，经常设计一个场景，然后通过渲染方程产生具有真实感的图像，因此需要引入几何造型（geometric modeling）技术来设计场景。如何在计算机中表示模型？这里我们介绍Bezier曲线和曲面。Bezier曲线曲面是非常重要的图形学理论，由法国工程师Bezier最初提出。

怎么表示曲线

物体表示方式主要有三种：

• 显式表示： $y=f(x)$
• 隐式表示： $f(x,y)=0$
• 参数表示： 图形学中最常用的。一个曲线的参数形式是通过一个自变量（参数）$t$来表示曲线点的每一个空间变量。在三维空间中： $$x = x(t)\ y = y(t)\ z = z(t)\ P(t) = [x(t),y(t),z(t) ]^T$$

参数形式的表示可以通过可视化点的轨迹随着$t$的变化来实现。我们可以将导数：
$$
\frac{dP(t)}{dt} = [\frac{dx(t)}{dt},\frac{dy(t)}{dt},\frac{dz(t)}{dt} ]^T
$$
看作为绘制的速度，导数为曲线切线方向。

参数曲线并不唯一。我们应当找出以$t$的多项式函数表达的参数形式。三阶多项式参数曲线具有如下形式：
$$
P(t) = at^3 + bt^2 + ct + d
$$
被称为Ferguson曲线。Ferguson曲线并不直观，给定各个参数，依然很难想象曲线的形状。

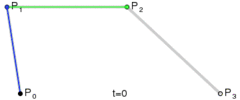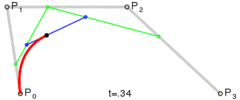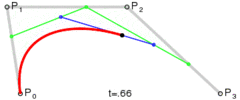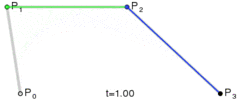
Bezier提出来利用几个向量来确定一个曲线，类似于先用直线勾勒出轮廓，然后根据这些向量生成曲线，如下图：

$$
V(t) = \sum_ {i=0}^n f_ {i,n}(t)A_i\ f_ {i,n} = \left {\begin{matrix} 1 & i=0\ \frac{(-t)^i}{(i-1)!}\frac{d^{i-1} }{dt^{i-1} }\left( \frac{(1-t)^{n-1} - 1}{t}\right) \end{matrix}\right.
$$
这个曲线定义很复杂，Bezier也解释不了为何这么定义。直到1972年Forrest才用数学解释了它的本质，他指出Bezier曲线可以借助于Bernstein多项式被定义到点集上。

Forrest说明，给定控制顶点$P_0,P_1,…,P_n$，则Bezier曲线可以被定义为：
$$
P(t) = \sum_ {i=0}^nP_iB_ {i,n}(t),t \in [0,1 ]
$$
其中，$B_ {i,n}(t)$是第$i$个$n$阶Bernstein多项式：
$$
B_ {i,n}(t) = C_n^it^i(1-t)^{n-i} = \frac{n!}{i!(n-i)!}t^i(1-t)^{n-i},i=0,1,…,n
$$

Bernstein多项式的性质

• 非负性
  $$B_ {i,n}=\left{\begin{matrix} =0 & t=0,1\ >0 & t\in{0,1} \end{matrix}\right. ,n = 1,…,n-1.$$
  对于端点($n = 0,n-1$时)：
  $$ B_ {i,n}(0) = \left{\begin{matrix} =1&i=0\ =0&otherwise \end{matrix}\right.\ B_ {i,n}(1) = \left{\begin{matrix} =1&i=n\ =0&otherwise \end{matrix}\right.$$

• 归一性 $$\sum_ {i=0}^n B_ {i,n}(t) = 1,t \in [0,1]因为： \sum_ {i=0}^n B_ {i,n}(t) = \sum_ {i=0}^n C_n^it^i(1-t)^{n-i} = [(1-t)+t]^n = 1$$

• 对称性 $$B_ {i,n}(1-t) = B_ {n-i,n}(t)$$
  证明： $$B_ {n-i,n}(t) = C_n^{n-i}t^{n-i}(1-t)^{i} = C_n^i(1-t)^{i}t^{n-i} = B_ {i,n}(1-t)$$

• 递归性 $$B_ {i,n}(t) = (1-t)B_ {i,n-1}(t)+tB_ {i-1,n-1}(t),i=0,1,…,n$$这表明$n$阶的Berstein多项式可以表示为$n-1$阶的组合，这就有了递归的条件。

• 导数
  $$
  B’_ {i,n}(t) = n [ B_ {i-1,n-1}(t) - B_ {i,n-1}(t)],i = 0,1,…,n
  $$
  根据导数我们可以求得极值：$B_ {i,n}(t)$在$[0,1]$之间有唯一的局部极大值：$x = \frac{i}{n}$。

• 升阶公式
  $$
  (1 - t)B_ {i,n}(t) = (1 - \frac{i}{n+1})B_ {i,n+1}(t)\ tB_ {i,n}(t) = \frac{i+1}{n+1}B_ {i+1,n+1}(t)\ B_ {i,n}(t) = (1 - \frac{i}{n+1})B_ {i,n+1}(t) + \frac{i+1}{n+1}B_ {i+1,n+1}(t)
  $$
  升阶公式很神奇。$n$只得是点的个数，这意味着同样的曲线可以对应更多的点（更多条边的控制多边形）。实际上点越多，就越接近曲线的形状，这是一个定理的一个例子：任何一条曲线可以用无穷多个线段来近似。

• 积分 $$\int 0^1B {t,n}(t)dt = \frac{1}{n+1}$$

Bezier曲线性质

• k阶导数的差分形式 $$P^{k}(t) = \frac{n!}{(n-k)!} \sum_ {i=0}^{n-k}\nabla^k P_i B_ {i,n-k}(t),t \in [0,1 ]$$高阶前向差分向量可以通过低阶前向差分向量递归定义： $$\nabla^0P_i = P_i\ \nabla^kP_i = \nabla^{k-1}P_ {i+1} - \nabla^{k-1}P_i$$
• 端点性质
  • 端点位置：根据Bernstein多项式的端点位置性质，可以得到： $$P(0) = P_0,P(1) = P_1$$因此得到的曲线的其实位置和控制多边形的起点和终点重合。
  • 切向量：因为$P’(t) = n\sum_ {i=0}^{n-1} P_i[B_ {i-1,n-1}(t) - B_ {i,n-1}(t)]$，所以得到： $$P’(0) = n(P_1 - P_0),P’(1)= n(P_n - P_ {n-1})$$,这意味着起点和终点处曲线的切向量方向与控制多边形的第一条和最后一条边的方向一致。
  • 二阶导数： $$P^{“}(t) = n(n-1)\sum_ {i=0}^{n-2}(P_ {i+2} - 2P_ {i+1}+P_i)B_ {i,n-2}(t)$$可以得到： $$P^{“}(0) = n(n-1)(P_2 - 2P_1 + P_0)\ P^{“}(1) = n(n-1)(P_n - 2P_ {n-1}+P_ {n-2})$$
    由曲率公式可得：
    $$k(0) = \frac{n-1}{n} \cdot \frac{\vert (P_1 - P_0) \times (P_2 - P_1)\vert}{\vert P_1 - P_0 \vert^3}\ k(n) = \frac{n-1}{n} \cdot \frac{\vert (P_ {n-1} - P_ {n-2}) \times (P_n - P_ {n-1})\vert}{\vert P_n - P_ {n-1} \vert^3}\$$
• 对称
  控制顶点为$P_i^{} = P_ {n-i}$的曲线保留了曲线$P(t)$的形状，但方向相反。 $$C^(t) = \sum_ {i=0}^n P_i^{ *}B_ {i,n}(t) = \sum_ {i=0}^nP_iB_ {i,n}(1-t)$$
• 凸包性质
  因为$\sum_ {i=0}^n B_ {i,n}(t) = 1, 0 \leq B_ {i,n}(t)\leq 1$，因此曲线$P(t)$在所有控制点的凸包内部。如下图：

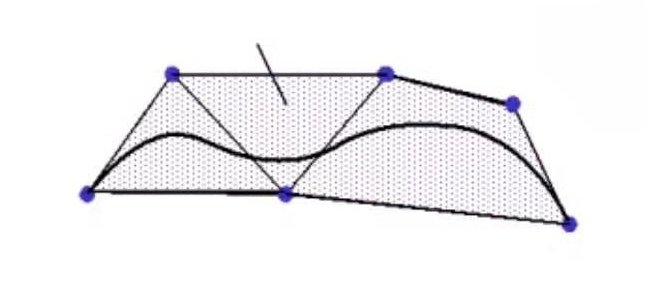
• 几何不变形
  几何性质不会随着坐标系变化而改变。Bezier曲线的位置和形状依赖于控制顶点$P_i$，而不是坐标系。

de Casteljau算法

我们当然可以通过计算Bezier曲线的值来得到，不过有一个更简单的算法来在计算机上画Bezier曲线。

首先注意到：
$$
\begin{aligned} P(t) &= \sum_ {i=0}^nP_iB_ {i,n}(t)\ &= \sum_ {i=0}^n P_i[(1-t)B_ {i,n-1} + tB_ {i-1,n-1}(t)]\ &= \sum_ {i=0}^n[(1-t)P_i + tP_ {i+1}]B_ {i,n-1}(t) \end{aligned}
$$
将上式的最后一步继续递归替换，直到$B_ {i,0}$，由此(具体过程没有推算，上一步也不清楚为何)我们最终可以得到Bezier曲线上一点的值为：
$$
P(t) = P_0^n
$$
定义$P_0^n$有递推公式如下：
$$
P_i^k = \left{ \begin{matrix} P_i & k=0\ (1-t)P_i^{k-1} + tP_ {i+1}^{k-1} & k=1,2,…,n;i = 0,1,…,n-k \end{matrix} \right.
$$
当$n=3$时，递推过程如下图：

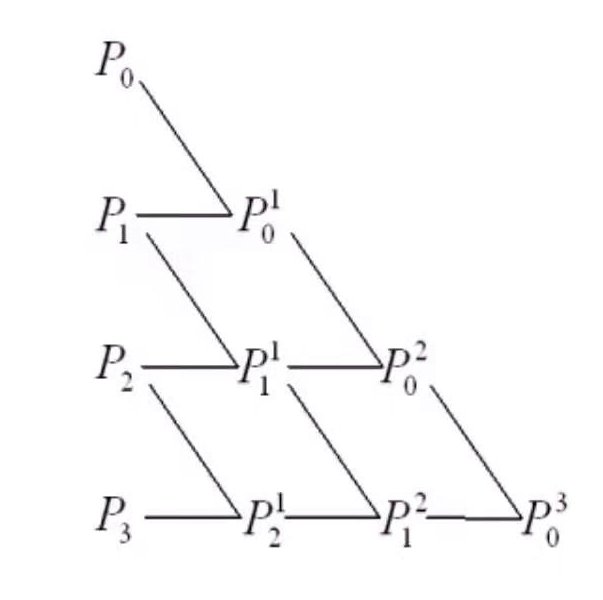
当我们需要知道某个$t$对应点的位置的时，最终需要知道的是$P_0^n$。需要注意，这里不是$P_0$的$n$次方，它的值是根据$t$计算出来的。

几何连续性

在CAD应用中，通常不鼓励通过高阶Bezier曲线来表达曲线，而使用光滑链接的低阶Bezier曲线。但是在Bezier曲线上，传统概念上的连续性不适用于图形学中几何的连续性。
比如两个点$V_0,V_1$分别定义下面的方程：
$$
\Phi(t) = \left{ \begin{matrix} V_0 + \frac{V_1 - V_0}{3}t & 0\leq t \leq 1\ V_0 + \frac{V_1 - V_0}{3} + (t-1)\frac{2(V_1 - V_0)}{3} & 1 \leq t \leq 2 \end{matrix} \right. \Phi(1^-) = \frac{1}{3}(V_1 - V_0), \Phi(1 ^+) = \frac{2}{3}(V_1 - V_0)
$$
上面的曲线实际是一条直线，但是却有两边导数不一致的情况。因此定义了几何连续性。

现在有两个分别由控制点$P_i$和$Q_j$定义的Bezier曲线。两个曲线共享端点，且：
$$
a_i = P_i - P_ {i-1},b_j = Q_j - Q_ {j-1}
$$

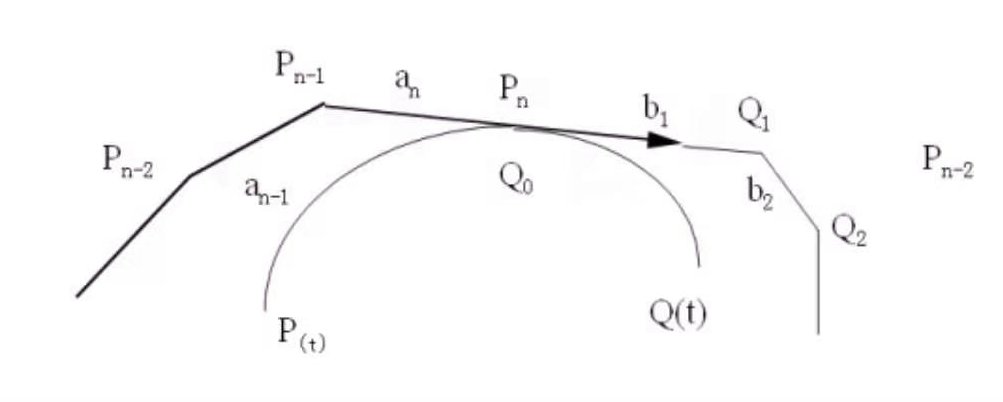
则：

• $G^0$连续：$P_n = Q_0$

• $G_1$连续：$Q_0 - Q_1 = \alpha (P_n -P_ {n-1})$，也就是$P_ {n-1},P_ {n},Q_0,Q_1$共线

• $G_2$连续（曲率连续）： $$Q_2 = \left(\alpha^2 + 2 \alpha + \frac{\beta}{n-1} + 1\right)P_n - \left(2\alpha^2 + 2 \alpha + \frac{\beta}{n-1}\right)P_ {n-1}+\alpha ^2 + P_ {n-2}\ Q^{“}(0) = \alpha^2 P^{“}(1) + \beta P’(1)$$

  升阶与降阶

前面在介绍Bernstein多项式的时候提到过升阶，对于Bezier曲线来说，升阶意味着通过增加控制点的方式来增加Bezier曲线的阶数，但保持曲线的形状和方向不变。

注意:
$$
\begin{aligned} P(t) &= \sum_ {i=0}^n P_iB_ {i,n}(t) = \sum_ {i=0}^n P_i ((1-t)+t)B_ {i,n}(t)\ &= \sum_ {i=0}^{n+1}\left(\frac{n+1-i}{n+1}P_i+\frac{i}{n+1}P_ {i-1}\right)B_ {i,n+1}(t) \end{aligned}
$$
可以得到升阶公式:
$$
P_i^* = \frac{i}{n+1}P_ {i-1}+\left(1-\frac{i}{n+1}\right),i=0,1,…,n+1
$$
如果$P_i$是$P_i^$升阶的结果，可以得到：
$$
P_i^{\times} = \frac{nP_i - iP_ {i-1}^{\times} }{n-i}; i = 0,1,…,n-1\ P_ {i-1}^ = \frac{nP_i - (n-i)P_i^*}{i}; i = n,n-1,…,1
$$
上面得到的也就是降阶的方法。我们有两种降阶方案:

• Forrest： $$\hat = \left{\begin{matrix} P_i^{\times} & i=0,1,…,\left [\frac{n-1}{2}\right ]\ P_i^* & i = \left [\frac{n-1}{2}\right ]+1,…,n-1 \end{matrix}\right.$$
• Farin： $$\hat P_i = (1 - \frac{i}{n-1})P_i^{\times} + \frac{i}{n-1} P_i^*$$

可以看到的是Farin是将Forrest的两个结果合起来。降阶除了直接升阶上去的，一般来说会有损失。

Bezier曲面

除了Bezier曲线还有Bezier曲面，曲面和曲线基本类似，但是形式更复杂，而且有两种，一个是矩形域，一个是三角域。

矩形域Bezier曲面

矩形Bezier曲面实际上本质依然是Bezier曲线。假设$P_ {ij}(i=0,1,…,n;j =0,1,…,m)$是$(n+1)\times(m+1)$的控制点集合，$n\times m$阶矩形域Bezier曲面可以通过张量积的形式定义：
$$
P(u,v) = \sum_ {i=0}^n\sum_ {j=0}^m P_ {i,j}B_ {i,n}(u)B_ {j,m}(v) , u,v \in [0,1 ]
$$
其中$B_ {i,n},B_ {j,m}$是Bernstein多项式。因此可以看到的是它是曲线的组合。

性质

• 端点：控制网格的四个顶点是Bezier曲面的顶点： $$P(0,0) = P_ {00},P(0,1) = P_ {0n}, P(1,0)=P_ {m0}, P(1,1) = P_ {mn}$$

以下三角形制定了四个角处的切平面：
$$
P_ {00}P_ {10}P_ {01}, P_ {0n}P_ {0,n-1}P_ {1n}, P_ {m0}P_ {m-1,0}P_ {m1}, P_ {mn}P_ {m-1,n}P_ {m,n-1}
$$

• 几何不变性

• 对称性

• 凸包

• 几何连续性

给定两个$n\times m$阶控制点为$P_ {ij},Q_ {ij}$的Bezier曲面：
$$
P(u,v) = \sum_ {i=0}^n\sum_ {j=0}^m P_ {ij} B_ {i,m}(u)B_ {j,n}(v)\ Q(u,v) = \sum_ {i=0}^n\sum_ {j=0}^m Q_ {ij} B_ {i,m}(u)B_ {j,n}(v)
$$
$G^0$连续：$P(1,v) = Q_0,v) or P(u,1) = Q(u,0)$，也就是公用一条边。

$G^1$连续：$Q_u(0,v) = \alpha (v) P_u(1,v) + \beta (v)P_v(1,v)$，也就是公用边两侧附近在一个平面上。

de Casteljau算法

与Bezier曲线一样，$P(u,v) = P_ {i,j}^{n,m}$。

$P_ {i,j}^{k,l}$通过以下递归公式定义：
$$
P_ {i,j}^{k,l} = \left { \begin{matrix} P_ {ij}& k = l = 0\ (1 - u)P_ {ij}^{k-1,0} + uP_ {i+1,j}^{k-1,0} & k = 1,…,n;l=0\ (1-v)P_ {0,j}^{n,j-1} + v P_ {0,j+1}^{n,j-1} & k = n;l=1,…,m \end{matrix}\right.
$$
或者：
$$
P_ {i,j}^{k,l} = \left { \begin{matrix} P_ {ij}& k = l = 0\ (1 - v)P_ {ij}^{0,l-1} + vP_ {i,j+1}^{0,l-1} & k = 0;l=1,…,m\ (1-u)P_ {i,0}^{k-1,m} + u P_ {0,j+1}^{k-1,m} & k =1,…, n;l=1,…,m \end{matrix}\right.
$$
对于de Casteljau算法的解释：
$$
\begin{aligned} P(u,v) &= \sum_ {i=0}^n\sum_ {j=0}^m P_ {ij}B_ {i,n}(u)B_ {j,m}(v)\ &= \sum_ {i=0}^n\left(\sum_ {j=0}^m P_ {ij}B_ {i,n}(u)\right)B_ {j,m}(v) \end{aligned}
$$
括号内部得到的是Bezier曲线。而曲面的de Casteljau算法也就是先计算一个维度上的曲线，计算到$0$开始计算另一个维度，直到递归至$P_ {i,j}^{0,0}$。

三角域Bezier曲面

三角域Bezier曲面定义在三角域，而不是方形域，使用重心坐标（barycentric coordinate）来定义三角域曲面。

• Bernstein基函数 $$B_ {i,j,k}(u,v,w) = \frac{n!}{i!j!k!}u^iv^jw^k; u,v,w \in [0,1]$$其中: $$u+v+w = 1,i+j+k = n;i,k,j\ge 0.$$有$\frac{1}{2}(n+1)(n+2)$个n阶基函数。

• 非负性和归一性： $$B_ {i,j,k}^n(u,v,w) \ge 0, \sum_ {i+j+k=n}B_ {i,j,k}^n(u,v,w) - 1$$

• 递归：

  $$B_ {i,j,k}^n(u,v,w) = uB_ {i-1,j,k}^{n-1}(u,v,w) + vB_ {i,j-1,k}^{n-1}(u,v,w) + wB_ {i,j,k-1}^{n-1}(u,v,w)$$

• 三角域曲面定义：
  $$
  \begin{aligned} P(u,v,w) &= \sum_ {i+k+j = n}P_ {i,j,k}B_ {i,j,k}^n(u,v,w)\ &= \sum_ {i=0}^n\sum_ {j=0}^{n-i}P_ {i,j,k}B_ {i,j,k}^n(u,v,w) \end{aligned}\ u+v+w = 1;u,v,w\ge 0$$

• de Casteljau算法 $$P_ {i,j,k} = uP_ {i+1,j,k} + vP_ {i,j+1,k} + w P_ {i,j,k+1}$$

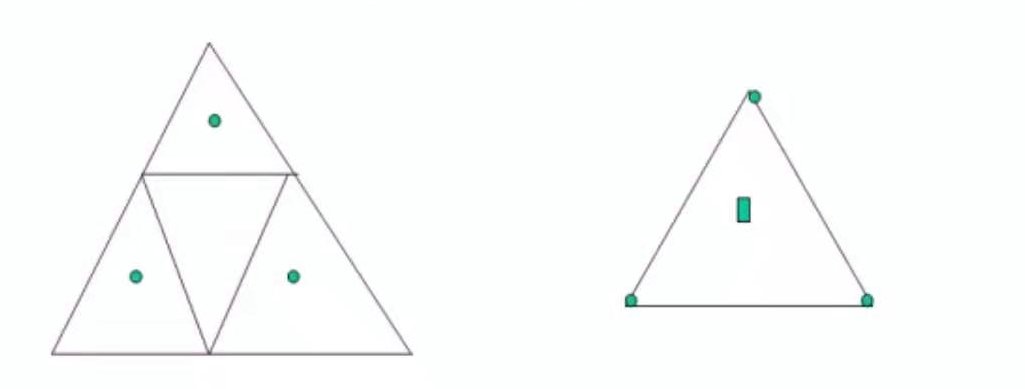
上面的算法看得不明白没关系，不过实际上三角域的de Casteljau算法非常简单。每三个点根据重心坐标算一个新的点，不断递归。