图形学——空间数据结构
上次讲了光线追踪,但是在追踪过程中,我们需要进行加速,可能才能满足实时等应用。同样,还有很多图形学的相关过程,都需要更好的数据结构的支持,用来加速和节省内存。下面介绍一些光线追踪时候用来加速的数据结构。
为了加速光线追踪,有多种数据结构。比如之前提到的包围体。包围体除了长方体,还有球体等等。也有比较熟悉的均匀grid用来表示空间点,四叉树和八叉树,kd树,hash表等等。
包围体
多组平行面包围体
包围体最简单想到的当然是长方体包围体,也叫包围盒,也是有多种的。最简单的为平行与坐标轴的包围盒。这个包围盒计算简单,但是效果很差,因为可能会多包很多地方。如下:

如何计算平行与坐标轴的包围盒?很简单,只要求模型里x,y,z方向上的最大值和最小值即可。但是正如上面所说的,这个包围盒太大,很多时候光线没有经过模型,但是经过了包围盒。因此我们需要更紧致一点的包围盒。

在计算更紧致的包围盒时,我们可以不局限与长方体,而是考虑用多组平行平面包围住一个模型。模型有两种情况,一种是网格模型,也就是由各个点构成,另外一种是隐士曲面,可能有无数的点。
用多少组平面围住模型更好?一般用5组就可以达到比较紧凑的效果,毕竟过多的平面会导致对包围体交点的计算也变的复杂。我们首先确定5组平面的法向量,然后尽量压缩这两个平面的距离。
首先,平面的方程为$Ax+By+Cz+d = 0$,而这一组平面对应的法向量为$n=(A,B,C)$。之前提到的,点距离已知平面的距离为:$d_0 = Ax+By+Cz+d$。因此我们规定这一组平面的原平面为:$Ax+By+Cz=0$,然后计算模型各个点投影到法向量$n$上后的点到原平面的距离,也就是$nP = Ax+By+Cz$。找到这个距离的最大值和最小值,也就确定了这一组平面。非常好理解。这个方法被称为Kay-Kajiya方法。
对于隐式曲面,也就是有一个方程$f(x,y,z) = 0$表示的曲面,可能有无数点。这时候点到原平面的距离不变,依然是$F(x,y,z) = Ax+By+Cz$,想要求它的最大和最小值,又加上了约束。因此,这个问题就变成了一个条件极值问题,使用拉格朗日乘数法就能很容易得到结果:
$$
\max F(x,y,z), \text{s.t. } f(x,y,z)=0
$$
包围球
另外一个常用的包围体是球形的。球形包围体有几个优点,它仅包含两个参数,球心和半径,而且具有旋转不变性。

然而计算最优包围球是很困难的,在这里介绍一个近似方法,它的时间复杂度为$O(n)$。一般来说,它比最优的包围球要大5%。
首先,遍历所有点,找到下面3对点:
x坐标最大的点,x坐标最小的点; y坐标最大的点,y坐标最小的点; z坐标最大的点,z坐标最小的点。
分别计算每一对点的距离,选择最大的距离作为包围球(s)的直径。但是这样并不一定能包围所有的点。因此还需要继续,如果发现了有在包围球外的点,将该点和原来包围球的球心连接并延长到球的表面,作为新的包围球(s’)的直径。不断重复上面的过程,直到没有点在包围球外部了。s与s’内切。
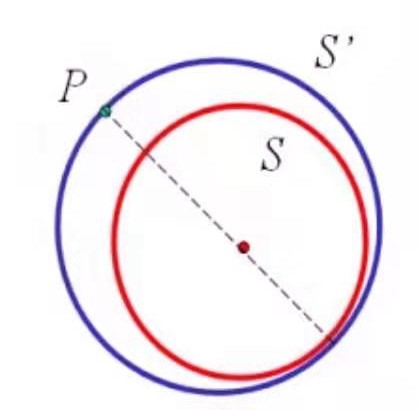
这个算法算不上优秀,因为它也需要不少的计算量,但是很容易理解。
层次包围体
一个包围体的比较好的拓展就是层次化。这个也很好理解。如果一个空间里有n个物体,每个都做包围盒,但是光线可能根本没有穿过这一块。因此,比较好的做法就是建立树状结构,对于各个空间块的物体建立层次包围体,每一层是对下一层的并集,如果上层没有交点,也就不用看下层了,从而大大减小计算量。这也是计算机科学中很重要的思想。
层次包围体一个有意思现象是,同层间包围体可能有overlap,但是这是无关紧要的。我们只需要保证上层完全包含了下层就可以。
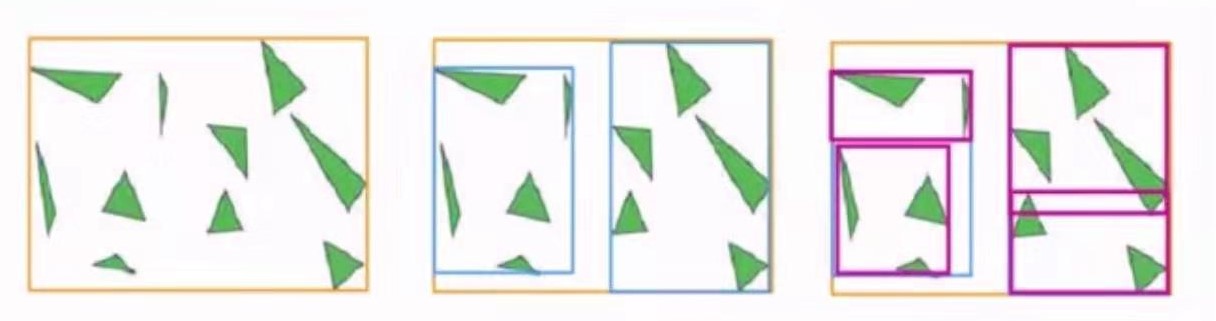
包围体除了加速,还在消隐,碰撞检测等等都有很重要的应用。
均匀格点(Uniform Grids)
均匀格点的想法,是通过将各个面片分到均匀网格中,然后计算出光线经过的网格(通过DDA算法),如果当前的格点中有面片,计算它和该面片的交点。它的优点在于,让光线自己去找,而不是对每个面片进行交点的计算。
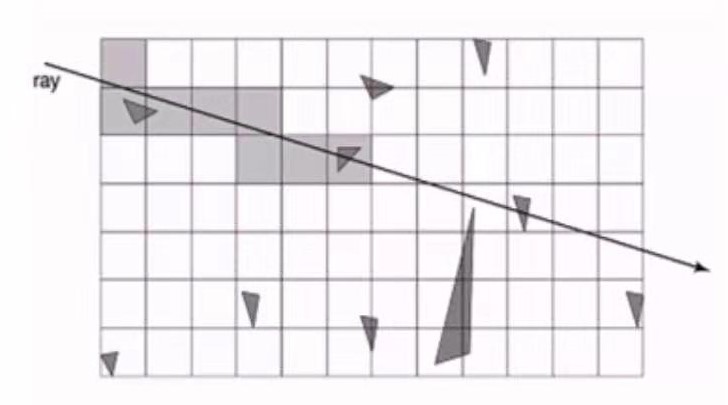
下面简单说明以下DDA算法。
DDA算法是二维的光栅算法,也就是在格点上绘制一条直线,也很容易拓展到三维。首先,二维中直线的方程为:$y=kx+b$,$k = \frac{dy}{dx}$。我们只要知道直线的两个端点,就能得到$k,b$的值。
同理,在平面上,像素也是一格一格增长的。知道直线方程,我们就能知道增加一格x,增加多少y:$x+1,y+k$,同理也知道,当y增加1,x增加$\frac{1}{k}$。
当我们知道$(x_i,y_i)$时,计算:
$$
x_ {i+1} = x_i + 1, \Delta y = k; y_ {i+1} = y_i +1 ,\Delta x = \frac{1}{k}
$$
比较$\Delta y,\Delta x$的大小,实际上就是比$k$和$1$的大小。
如果$k>1$,则说明y走得更多,则选择让y的步长为1:$y_ {i+1} = y_i+1, x_ {i+1} = x_ {i} + \Delta x$。然后对$y_i,x_i$进行向下取整,得到坐标。
如果$k<1$,则选择让x的步长为1。
下面简单写一个python代码实现下二维的DDA算法吧。
1 | import math |
这个程序会生成一张白色图片,根据你输入的k,以$(50,50)$为起始坐标,利用DDA算法生成一张直线图。为了简化,只写了$k>0$的情况。下面是$k=0.6$的情况:
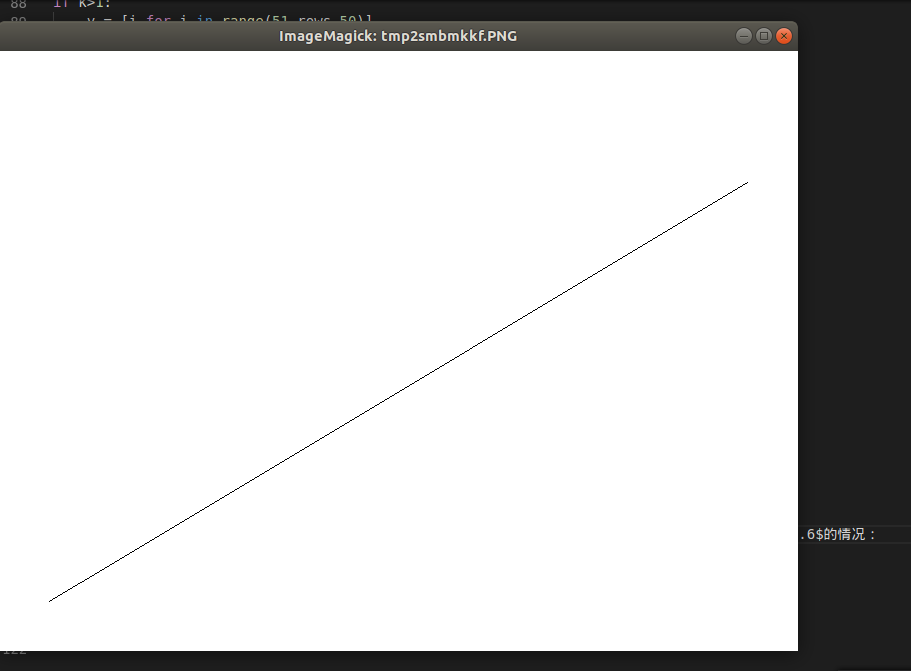
查看细节:

如果想要查找有光线经过的网格,将上述代码中注释的部分去掉即可。在使用DDA算法时候,我们设定速度更快的那个轴步长为一,然后计算另外一个轴的值来向下取整,但是这样会导致一部分光线经过的方块没有画出来。如果另外一个轴的值本身就是整数,则不会出现这种情况。因此,判断该值是否是整数,然后进行相应处理。
画出有光线经过的网格的结果如下:
可以看到,这个线变“粗”了。

下面是三维中均匀格点的方法的可视化:
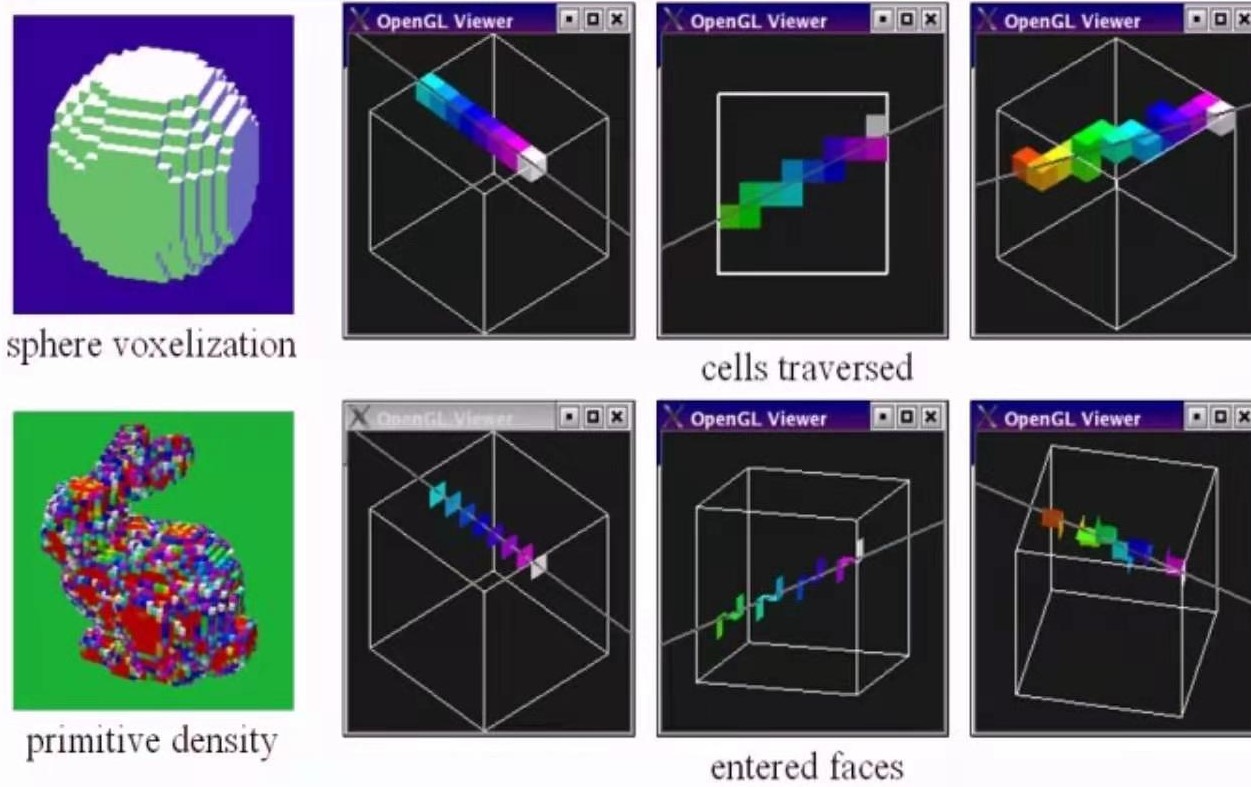
均匀格点的有点是容易构建,也容易遍历,想法也简单,但是它的缺点在于,都是均匀的,有时候大多数多边形只占一小部分,一个格子格子遍历速度是很慢的。格子过大,每个格点中面片过多,使得运算变慢,而格子过小,又会导致大量的存储问题,速度也不快。
由于空间中物体分布就是不均匀的,因此均匀格点没那么合理,非均匀的格点是更好的选择。
八叉树(Octree)
八叉树是四叉树的推广,四叉树是二叉树的推广,分别对应着三维,二维,一维的情况。
八叉树我之前在写一个小的SFM程序时曾经用过,用它来加速计算的过程。现在讲一讲它在光线追踪过程中的应用。
首先,八叉树的目的,是在面片比较多的空间中,用更小的格点去表示,也就是更高的分辨率,而在面片比较少的空间中,用更大的格点表示。最基本的划分,是将一个空间正方体,根据三维坐标系的8个象限分成8个方块,对需要细分的方块继续进行8叉树的划分。
值得注意的是,一般的8叉树,对于多面体的表示可能是重叠的,也就是可能一个多面体有一部分在这个格子,另一部分在另一个格子。这种情况下,有多种做法,一是重复包含,也就是将每个格子只要包含了部分这个面片,就记它包含了这个面片,这种情况的比较明细的缺点,就是加大了计算量;第二种是将面片按照空间的划分切割,这个做法也不是太好,因为也比较复杂,会切割出更多的面片,使得面片总数增加,也增大了计算量;第三个是用一种改进的八叉树,叫做Octree-R,它使得空间划分更自由一点,相对于最naive的做法,可以提速10%~47%。本篇文章仅仅说明最简单的八叉树,不考虑面片重复的情况。
如下图:
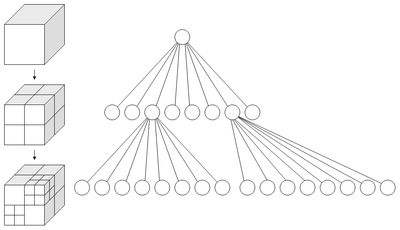
八叉树的建立是这么一个过程。首先,将整个空间分成8个方块,计算每个方块中的面片个数,如果面片个数大于某个阈值,就对该空间继续进行同样的细分,直到方块中包含的面片个数小于某个阈值,或者达到了最大的递归深度,就退出递归。而八叉树的最小方块的分辨率,被称为这一颗八叉树的空间分辨率。
八叉树比较厉害的一个点,是对各个方块进行层次编码。如果八叉树的深度为$N$,八叉树终结节点(叶子节点,也就是各个方块)的编码为$\underbrace{q_1q_2…q_iF…F}_N$。只有第N层的深度的叶子节点,才能编码中所有的都是$0~7$的数字,而对于层次未达到N层的叶子节点,为了保持编码长度一致,后面的几个位置编码用$F$(可以用任何字母)表示。规定了下图这样的编码方式,给定空间中的任何一个坐标,我们可以迅速定位到这个坐标所在方块的编码。
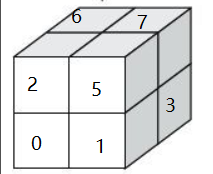
也就是给x轴权重为1,y轴权重为2,z轴权重为4。
如果我们得到一个空间点的位置$P(x,y,z)$,要注意的是这里的$x,y,z\ge 0$,而且为整数。但是实际情况中,坐标不一定是正整数,因此这里的坐标点是经过处理的相对坐标,正如一张图片的坐标一样。
我们分别将$x,y,z$写成二进制形式:
$$
x = {i_1i_2…i_N}_ {B},y = {j_1j_2..j_N}_B,z = {k_1k_2…k_N}_B,
$$
则它属于的空间块的编码为:
$$
q_n = i_n + 2\cdot j_n + 4 \cdot k_n, n = 1,…,N
$$
匹配规则采取最长匹配,只要没碰到$F$或者算完$N$位,就计算下去。
同理,我们可以根据方块的编码$q_1q_2…q_MF…F$,得到方块中的空间坐标二进制前$M$位的值:
$$
i_n = q_n& 1, j_n = q_n & 2, k_n = q_n & 4, n = 1,…,M
$$
下面说,如何通过八叉树来加速光线追踪。首先,利用上述性质,根据光源坐标来求光源所在的方块编码$Q$,然后计算方块中面片与光线是否有交点。如果有的话很好,就结束了,如果没有,那么光线会射出这个方块。这里稍微复杂一点。首先,要用光线对着6个面求交,然后利用光线的截距和斜率,得到它在下一个起点,作为光源点,计算所在方块编码,重复上述过程,直到射出八叉树的范围,或者找到交点。
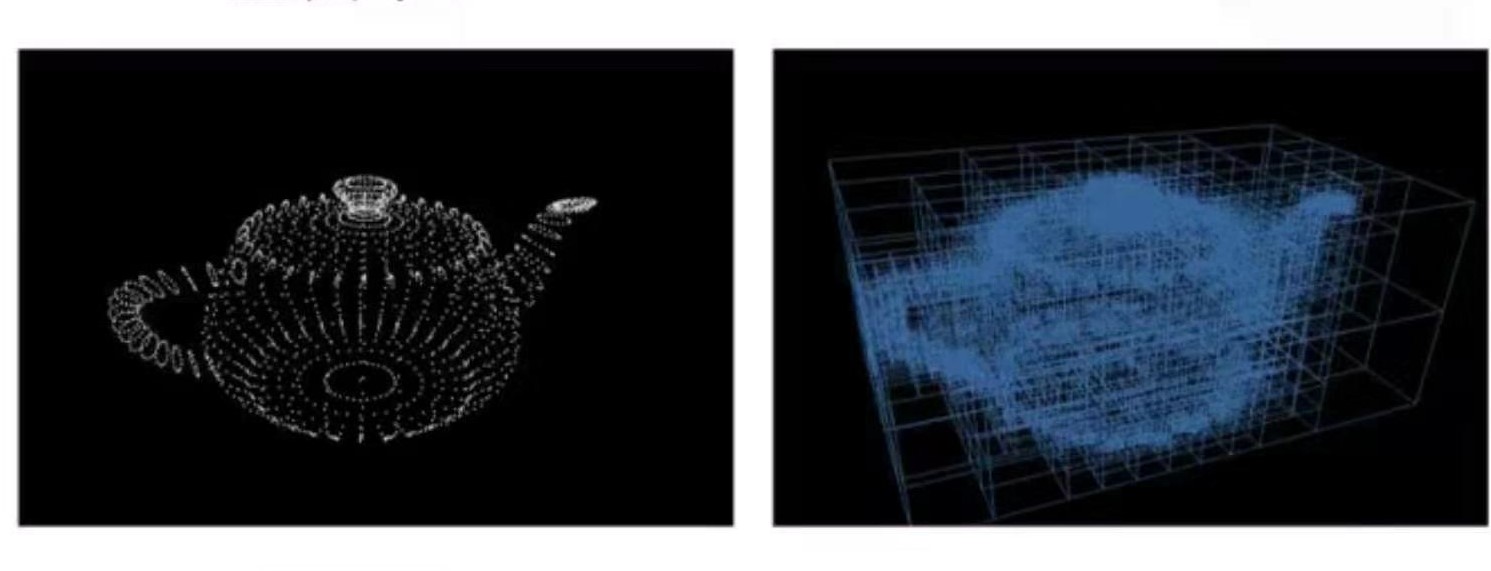
八叉树的建立看上去稍微繁琐,但是在空间分布不均匀而且面片非常多的情况下,可以非常显著地提高追踪的速度。下面是一个用八叉树表示的例子:

BSP树和k-d树
二叉空间分割树(BSP)是另一种方法,它和八叉树不同,它每次用一个平面将空间分成两部分,最初用来解决隐藏表面问题。它主要有两种类型:axis-aligned与polygon-aligned。axis-aligned也就是根据坐标轴来分割空间,而polygon-aligned是根据多边形来划分,实际上就是根据某个面片的所在平面来划分。很明显,axis-aligned更简单,在这里我也主要说明axis-aligned。
划分平面的正交性极大简化了光线与划分平面的求交运算,光线与一个Axis-aligned的平面求交计算量是与任意位置的平面求交的$1/3$(统计数据)。
BSP的构建过程和Octree是非常类似的,每次使用一个垂直于坐标轴的划分平面将一个当前的叶子划分为相等的两个节点,如果未达到递归终止条件(面片个数小于阈值或者深度大于最大值),则继续划分。当然,每次划分的时候选取垂直的坐标轴是不一样的,如果一直使用一个坐标轴,得到的就是很细的切片。
下面是一个BSP树存储的例子:
而k-d树与BSP树的区别在于,k-d树对于节点的划分不要求是相等的,BSP树是k-d树的一种特殊情况。光线在BSP树中的遍历就不多说了,因为具体的我也不了解。它的思想和Octree应该差的不多,通过坐标可以快速定位到点所在的叶子节点,因为每次比较的只有一个坐标轴的值。在实际中光线遍历BSP树的速度会比Octree快10%左右。和Octree一样,某个面片可能出现在多个划分中,与Octree-R的思想类似,它可以用K-d树来解决。
其他技术
还有很多更高级的光线追踪技术,这里简单提一下:
- 分布式光线追踪,举个例子,反射的时候传统算法只会朝着一个方向反射,而分布式会在一个范围内反射,可以实现软阴影等效果。
- 光束追踪,将多个像素融合成一个光束,包含了局部坐标和世界坐标的转换
- 选择性光线追踪,选择一些点进行光线追踪,然后对其他的点进行插值,可以加快计算,但是会变得模糊一点
- 基于小波的像素选择,通过小波来进行重要性采样,选择重要的像素来进行追踪