图形学——光照模型

Posted on 2019-03-12 Edited on 2023-10-21 In 图形学

这次简单介绍一下几个著名的光照模型。

首先，我们要知道，我们能看到物体是因为物体反射的光进入了我们眼睛。光照模型是基于入射角反射角定理的。在物理上有一个更复杂一点的描述光的反射的函数，简称BRDF（双向反射分布函数）。因此这些光照模型，又被称为BRDF模型。

再介绍各个模型之前，我们再了解一些关于光学的定义。入射角反射角定理就不多说了，是中学知识。光有以下几个度量方法：

立体角：
- 衡量物体相对于某一视点P的视角大小：$dw = \frac{ds}{r^2}$，距离为弧面面积比上距离的平方
- 立体角最大为$4\pi$，也就是球面积比上半径的平方
光通量：
-光通量为单位时间内通过面元$ds$的光能量，记为$dF$
发光强度：
-发光强度为单位立体角内的光通量，记为$I$

我们知道能量守恒定理。在光反射的过程中也是一样的，光的能量等于被镜面反射的光的能量，漫反射的光能量，如果有折射还要加上折射掉的能量，以及被物体吸收等所有能量之和。

Phong模型

Phong模型是最简单而且也是最常用的光照模型。它支持点光源和方向光源。Phong模型是局部光照模型，它将局部光照效果简单分解为下面三个部分：

漫反射光效果
镜面反射光效果
环境光效果 I_i = I_d + I_s + I_a.如下图：

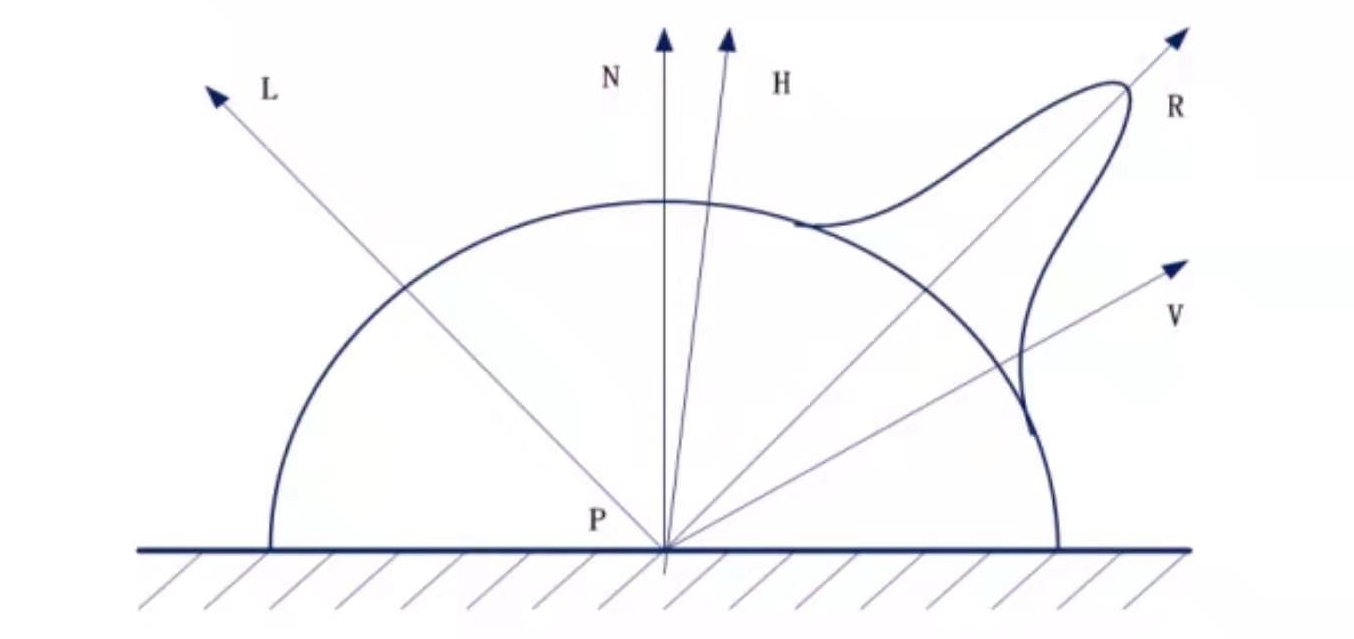
L为入射光方向（图中方向画反），R为反射光，N为物体表面法向量，V是视点方向，H是L和V夹角的角平分线方向。

漫反射光效果

漫反射光的传播是各项同性的
漫反射光强度为：I_d = I_iK_d\times (L\cdot N)上式中$K_d$为漫反射系数，具有3个分量，分别代表R，G，B三个通道的漫反射系数。可见，$K_d$与模型自身的色彩紧密相关。

镜面反射效果
对于光滑的平面，根据反射定律，反射光往往集中在一个小的立体角内，这些反射光我们称之为镜面反射光。
镜面反射光的强度为： I_s = I_iK_s \times (R\cdot V)^n上式中，$K_s$为镜面反射稀疏，与物体表面的光滑程度有关，而$n$是反射指数，$n$越大，高光区域越集中，这里的意思是，因为$R \cdot V$是小于等于1的，如果$n$越大，$(R\cdot V)^n$下降得越快，因此高光越集中。

环境光效果

环境光效果很简单，也就是除了镜面反射和漫反射的其他光总称为环境光。$I_a = I_iK_a$。

所以Phong模型非常简单，它简单将光分成这几类，计算量很小，而且保证了不错的效果。因此被广泛使用。

法向插值

当然，明暗处理（shading）除了光照模型这些，还需要考虑的是插值。因为物体表面几个细节并不规则圆滑，为了减轻这种效果，需要对面片进行插值。插值也有多种方法，在Phong之前采用的是颜色插值。而Phong采用了一种新颖的想法，对法向进行插值。得到面片上各个点（非顶点）的法向，这时候在进行光照处理，会使得整个模型显示更加平滑。很神奇的是，我们先通过顶点计算出面片法向，再通过面片法向计算出顶点法向，然后根据顶点法向对面片上各个点法向进行插值，它们在互相利用。

其他BRDF模型

这里将除了Phong模型以为的模型归结为其他，是因为我的知识浅薄，对其他的模型理解的不够透彻，绝对不是因为他们不够重要。对于要求更高的场景Phong模型是肯定不够的。其他的模型一般有更好的效果，相应也更复杂一点。

一般来说，BRDF模型有物理模型和经验模型两个区别。其实这个分类也不是太绝对，因为即时是经验模型也是基于一些物理知识的。

经验模型一般是依照直觉来定一些规则，而物理模型是严格按照光学物理知识来建立模型。

菲涅尔项

在物理模型中，会假如一个菲涅尔项，是基于一个物理的现象：单向反射性在擦地角附近增大。在一般物理模型中，入射光的反射量是由麦克斯韦电磁波方程组中的菲涅尔公式得到的，被称为菲涅尔项。菲涅尔项的定义比较复杂，如下：

比较著名的其他光照模型还有Cook-Torrance模型，Ward模型（各向异性，没有考虑菲涅尔项和衰减稀疏，更像是经验模型）。

除了物理模型和经验模型，还有一种是基于数据的，数据驱动模型。原理就是采集大量数据，获取光的规律。它一般需要很大的数据集，并且需要数据降维来压缩数据。