Paper——Large-Scale and Drift-Free Surface Reconstruction Using Online Subvolume Registration
这次周末再读一篇文章,希望能从中得到一些启发,来做好现在的相关的工作。这篇文章为Large-Scale and Drift-Free Surface ReconstructionUsing Online Subvolume Registration,是2015年CVPR的一篇文章。
关于TSDF,我们已经知道的很多了。在这篇文章中也是同样的。文章中,$\mathbf{u}$代表空间中的三维点,而$F(\mathbf{u})$代表该点的SDF值,$W(\mathbf{u})$表示的是SDF值的信心度量(可以理解为权重)。不同的地方是,文章中还定义了一个归一化梯度:
$$
\hat{\nabla}F(\mathbf{u}) \triangleq \frac{\nabla F(\mathbf{u})}{\Vert \nabla F(\mathbf{u}) \Vert}
$$
当$F$是常数时,返回一个未定义值。
问题描述
为了进行depth fusion,每个voxel都被投影到二维平面中,并且和传感器获得的深度值对比:
$$
\Delta _z(\mathbf{u},t) = D_t(\pi (T^{-1}_t \cdot \mathbf{u})) - \zeta(T^{-1}_t\cdot \mathbf{u})
$$
上式中,$\pi$是一个$\mathbb R^3 \rightarrow \mathbb R^2$的投影过程,也就是从三维到二维的转换,而$\zeta$提取了$z$坐标,也就是$\zeta(x,y,z) = z$。当$\Delta_z > -\sigma$时候更新TSDF值,而$\sigma$指的是截断距离。新的TSDF$(F^{new},W^{new})$为:
$$
F^{new}(\mathbf{u}) = \frac{F(\mathbf{u})W(\mathbf{u})+ \min\left(1,\frac{\Delta_z(u,t)}{\sigma}\right)}{W(\mathbf{u})+1},\ W^{new}(\mathbf{u}) = W(\mathbf{u})+1
$$
值得注意的是,这里依然保留的是截断距离,只不过用了另一种方法,选取和1比较的最小值。另外,对于权重的分配,有很多种方法,论文中采取的是最简单的,也就是平均分配,每次$W = W+1$。
这篇文章的模型是在KinectFusion的基础上进行的,而KinectFusion之所以不能很好的在large scale上应用,主要有两个原因,一是drift累积,二是global TSDF会需要较大的内存。
Low-Drift局部模型
这篇文章在解决Drift问题上,采取了submap的形式。在本文中,称为subvolume。每K帧会建立一个submap。这篇文章提出了一个比较有趣的方法,来做integrate,为了避免每一步都进行K次integrate,也就是对F,W的更新,每次得到新的帧时,它将该帧以及对应的位姿push进一个队列中(FIFO),同时将$t-K$帧pop出去,对TSDF volume进行腐蚀(erosion):
$$
F^{new}(\mathbf{u}) = \frac{F(\mathbf{u})W(\mathbf{u})-\min\left(1,\frac{\Delta_z(u,t-K)}{\sigma}\right)}{W(\mathbf{u})-1},\ W^{new}(\mathbf{u}) = W(\mathbf{u})-1
$$
当处理的帧数量少于K帧时,不会发生腐蚀。当到达K帧时,队列也满了,将volumen从GPU拷贝到主机中,作为一个新的subvolume,然后腐蚀操作开始。其实我是真的不知道这样做有什么吊用。。。或者我理解有误?总之,这不是关注的重点。
这一部分还包含了对有效Block的筛选,也是比较常规的做法,就不多说了。
本文中$K=50$。
Subvolume注册
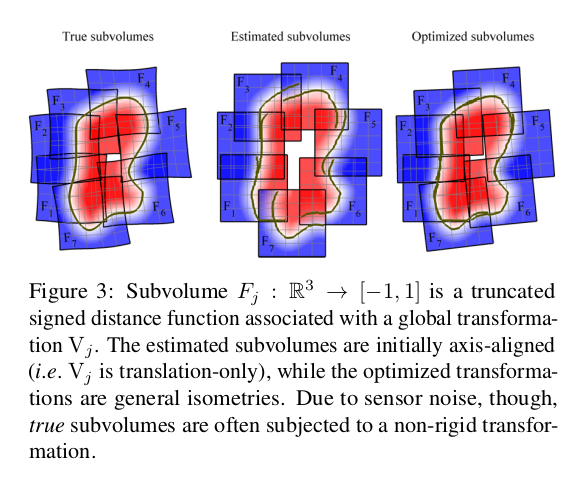
在本文中,每K帧形成一个新的subvolume$(F_j,W_j)$,被存储在主机上,下面会将各个subvolume的位姿表示为$V_j$。尽管每个subvolume的局部位姿都很小,但是将它们直接简单收集起来会产生较大的drift和misalignment。本篇文章中通过全局优化各个subvolume的位姿来解决这个问题,当得到一个新的subvolume时,会通过一个创新的volume混合方案来进行非刚性变换。一个比较显著的点是,这个优化过程不需要相机tracking模块,因此它可以使得操作实时进行,并且在把新的subvolume放入一个共享缓存区,允许位姿优化作为一个并行运行的过程。
提出的优化过程是受到了ICP算法的启发。优化需要的cost function是这样得到的:
- 对于每个subvolume,提取出zero-level的点的集合,并且得到它们的法向量
- 对于每个subvolume,考虑它的边界框,并且找到与其他subvolume之间的overlap
- 对于每个subvolume得到的点集,通过距离函数的梯度来找到与它有overlap的subvolume中的对应
- 每个有效的对应都会带来一个点到平面的距离约束,用来优化
- 如果有一个位姿超出约束,至少有一个位姿错误项被添加,来保证全局一致
接着,通过最小化一个合适的cost function来优化subvolume的位姿。在添加subvolume时候,上一个创建的subvolume的位姿保持固定,来得到tracked相机的最终估计。相对应的,下一个subvolume也能很快根据之前的subvolume得到一个合适的位姿,在相机track成功的情况下。cost funtion会最小化直到收敛,当得到新的对应时,继续最小化。下面会详细介绍一下point matching和优化问题。
The Correspondence Set
给定subvolume$(F_j, W_j)$,以及zero-level点集:$\left{ \mathbf p_i^{(j)} \right}$以及计算的法向量$\mathbf{n_i^{(j)} } = \hat{\nabla}F_j\left(p_i^{(j)}\right)$。我们定义最小的边界框(bounding box)包围了它所有的有效voxel。接着,找到subvolume的子集$S^{(j)}$,它们之间有重叠的边界框。接着,对于每个点$\mathbf p_i^{(j)}$,我们遍历候选集,对于每个$k \in S^{(j)}$,计算插值距离函数以及它在$V_k^{-1} \cdot V_j \cdot\mathbf p_i^{(j)}$的梯度。如下图:
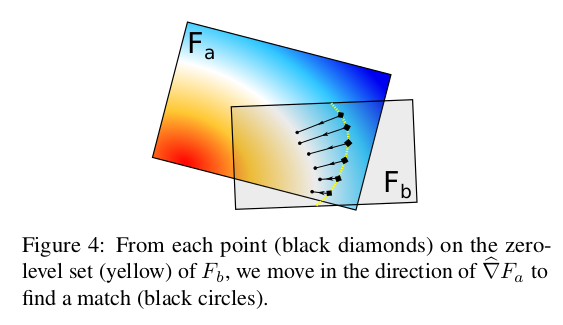
一个点的match为下:
$$
\mathbf q_k^{ij} = V_k^{-1} \cdot V_j \cdot \mathbf p_i^{(j)} - F_k\left(V_k^{-1} \cdot V_j \cdot \mathbf p_i^{(j)}\right)\hat \nabla F_k\left(V_k^{-1}\cdot V_j \cdot \mathbf p_i^{(j)} \right).
$$
对于所有的subvolume中所有的采样点进行上面的过程,有点类似于ICP算法匹配的过程。我还不是很明白这里梯度那一项的作用,也许可以增加鲁棒。
The Opitimization Problem
假设通过上面的过程,我们已经成功找到了对应。我们可以根据这些对应建立cost funstion。对于每个点对$\left( \mathbf p_i^{(j)},\mathbf q_k^{ji} \right)$,我们对$F_k$在$\mathbf q_k^{ji}$处的形状是没有保证的。我们已经估计了$F_j$中$p_i^{(j)}$处的法向量,因此我们可以得到一个点与平面之间的constraint:
$$
e_k^{ji} = \left(\mathbf p_i^{(j)} - V_j^{-1}\cdot V_k \cdot \mathbf q_k^{ji}\right)\cdot \mathbf n_i^{(j)}.
$$
cost function的形式为:
$$
\arg \min_ {V_1,…,V_N} \sum_j \sum_i \sum_k\Vert e_k^{ji} \Vert^2
$$
在本文中,通过Ceres中的列文伯格-马夸尔特方法来优化。
在这个过程中,有可能会出现一些别的情况,比如subvolume $F_h$是空的,或者有很少的基数,使得约束不成立,或者得到很差的位姿估计,在这种情况下可以引入位姿之间的约束来增强相机追踪得到的估计。当这个位姿引用的两帧分别在两个subvolume上,如$Z_ {h-1,h}$,则估计的错误项可以描述为下:
$$
e^{h-1,h} = \Phi\log (Z_ {h-1,h} \cdot V_h^{-1} \cdot V_ {h-1})
$$
上式中$\log$将$SE(3)$转换到$\mathcal{se}(3)$,而$\Phi$是一个$6\cdot 6$的刚性矩阵。按照经验将$\Phi$设置为单位矩阵。
融合Subvolume
对于融合Subvolume,文章中没有过多介绍。如何融到一个global volume中?
$$
F_G(\mathbf u)=\frac{\sum_j F_j(V_j^{-1}\cdot \mathbf u)W_j(V_j^{-1}\cdot \mathbf u)}{\sum_ {j}W_j(V_j^{-1}\cdot \mathbf u)}.
$$
这个过程并没有比较新奇的地方。文章中,如何融合global volume,是通过对一个全局的位置依次扫描,对每个位置$\mathbf u$进行上述的操作。这样的采样,如果subvolume分布比较广,会导致大量的无用计算。如下图:
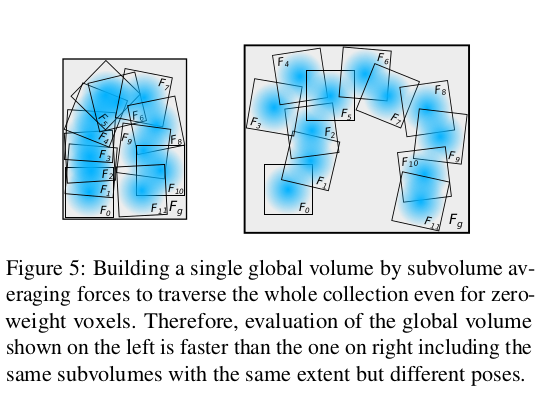
因此,它会根据有overlap的subvolume来进行:
$$
F_j(\mathbf u) = \frac{\sum_k F_k(V_k^{-1} \cdot V_j \cdot \mathbf u) W_k(V_k^{-1} \cdot V_j \cdot \mathbf u)}{\sum_kW_k(V_k^{-1}\cdot V_j \cdot \mathbf u)}.
$$
上式中$k \in S^{(j)}$,也就是与subvolume j有重叠的subvolume的集合。
上述就是这个文章的主要内容。其实读完了我觉得没什么特别新颖的点。