RANSAC——随机采样一致
RANSAC(RANdom SAmple Consensus),随机采样一致,是一个比较简单,但是在SLAM,图像陪准中用得很多的算法。当然,在这里我们专注于算法的本身,至于它在其他的地方的应用要结合具体情况分析。
假如现在有一组采样得到的点,是由一条直线生成的。但是由于噪声的存在,它变得很乱。现在我们希望恢复这条直线。如果噪声比较小,或者是高斯噪声,我们使用最小二乘法(线性回归)就可以得到最佳的那条线,它们都用了least squares作为要优化的目标(可以看数据学习第一篇)。但是噪声比较大,而且我们也不知道噪声生成的规律,那么这个问题使用线性回归可能就得不到我们想要的那条线,因为此时least squares用作cost function不合适了。比如下图:
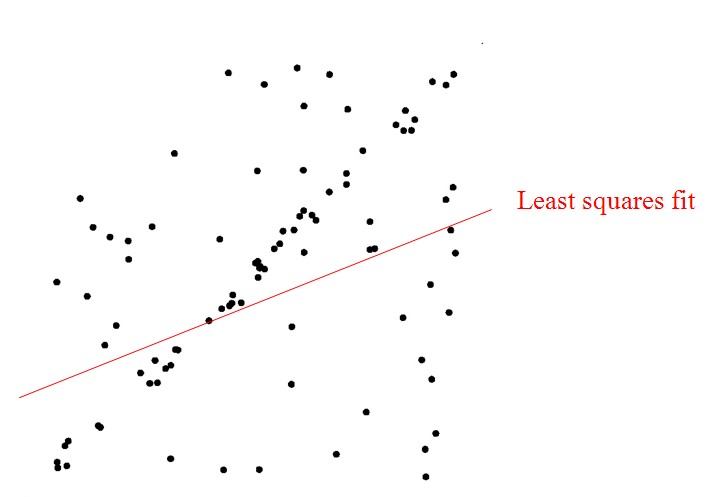
我们可以很轻易的看出来这个线应该是什么样子,但是使用线性回归却得到了错误的结果。
RANSAC算法的思想非常简单,它认为,有更多的样本符合这个假设,这个假设就是正确的。但是如何让最多的样本符合这个假设应该是一个NP-hard的问题,正如PLA中,如何分类使得错误的个数最小。
RANSAC算法是这么做的,随机采取一定的点来确定这个模型,正如本例中,两个点就可以确定一条直线。当然,实际上我们不会只采两个点,而是采一组,用这一组点利用线性回归或者最小二乘法得到模型,然后定义一个distance的threhold,对于小于threhold的确定为局内点(inlier),对于大于的定为局外点(outlier)。根据inlier的个数来觉得这个模型的好坏,并且重新计算这个模型。
不断迭代上面的过程,进行随机采样,如果可以得到更好的模型,就用它来替换最好的模型,如果不行,就将其淘汰,算法过程如下图:
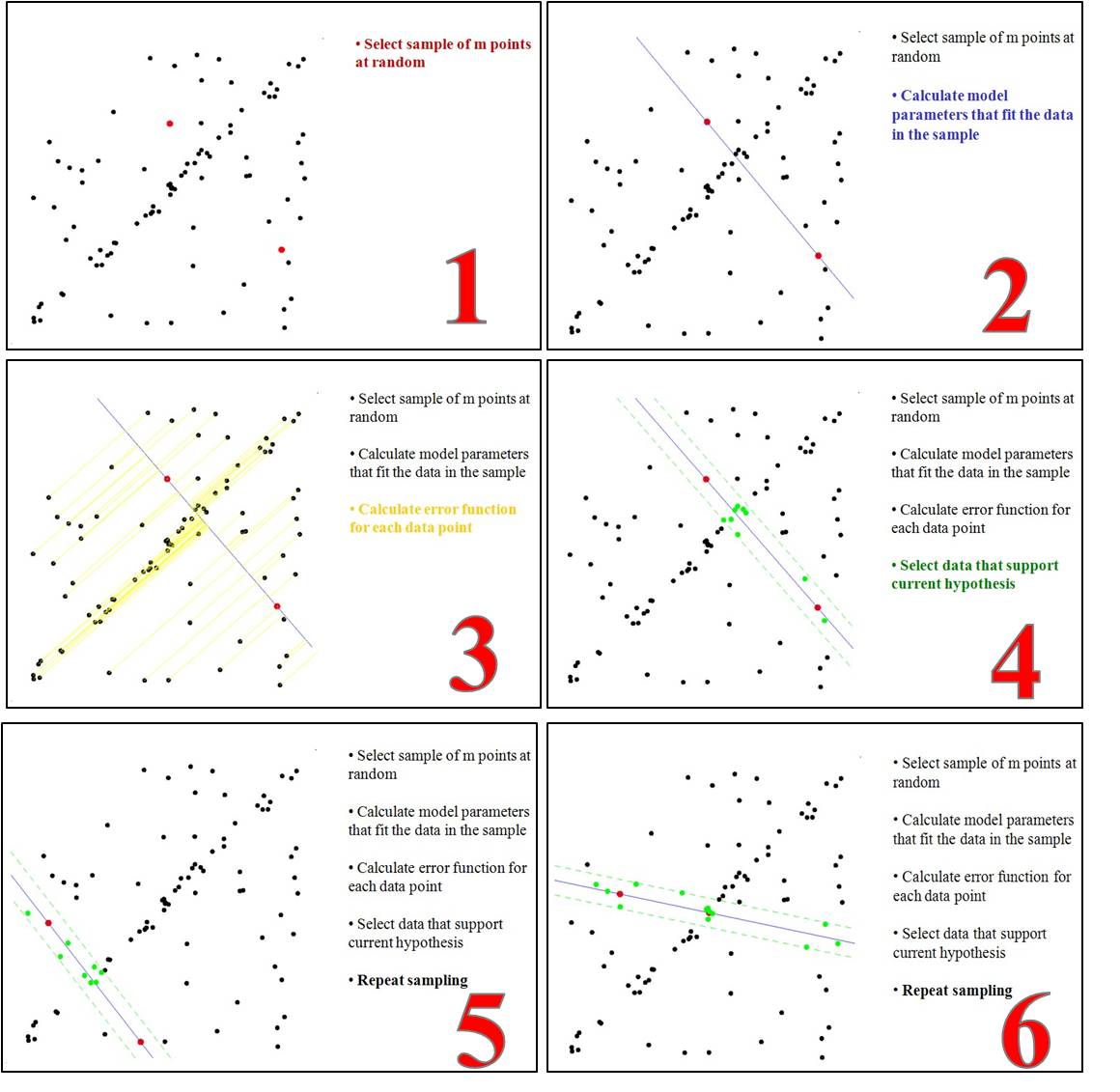
可以看到的是,我们不能保证RANSAC收敛,因此会一般执行一定的步骤,得到最后的结果。在很大概率下,Ransac是可以得到不错的结果。实际上它的思想和Pocket PLA是非常相近的。
下面我们提一下Ransac在图像特征匹配中如何剔除误匹配。我们根据随机选取几组匹配点可以计算出一个位姿,也就是利用八点算法,或者五点算法。要知道一般来说误匹配的个数是相对正确的来说比较小的,因此理论上大部分的匹配点都应该满足这个位姿。接着我们看匹配点有多少是符合这个匹配的。不断迭代上面的过程,最后可以选取一个相对之前的多次迭代采样来说最正确的位姿,剔除掉不符合这个位姿的匹配点即可。在SLAM中的对于位姿的估计也是相似的做法。