信息论——信息速率失真函数与熵压缩编码(二)
之前说到,我们直觉构造的1比特下高斯信源的传输与理论上的失真还有点差距,需要进行分组才能得到最优。下面,我们用失真联合典型序列来证明,同时证明率失真定理。 率失真定理的核心是我们要证明$R(D) = R^{(I)}(D)$。
率失真定理的converse
与之前不同的是,我们首先来证明定理的逆。我们需要说明这样一件事:
对于服从分布$P(x)$的随机变量$X$和失真度量$d(x,\hat x)$,以及任意满足失真小于$D$的率失真编码$(2^{nR},n)$来说,$R \ge R^{(I)}(D)$。
如下图:

我们证明的是可行域是如图所示的。
$$
\begin{aligned} nR &\ge H(\hat X^n)\ &\ge H(\hat X^n) - H(\hat X^n|X^n)\ &= I(\hat X^n,X^n)\ &= H(X^n)-H(X^n|\hat X^n)\ &= \sum_ {i=1}^n H(X_i) - \sum_ {i=1}^n H(X_i|\hat X^n,X_1,…,X_ {i-1})\ &\ge \sum (H(X_i) - H(X_i|\hat X_i))\ & = \sum I(X_i;\hat X_i)\ & \ge \sum R^{(I)}(E[d(X_i,\hat X_i)]) \ &= n\sum \frac 1 n R^{(I)}(E[d(X_i, \hat X_i)])\ &\ge nR^{(I)}(\frac 1 n \sum E[d(X_i,\hat X_i)])\ &= nR^{(I)}(D) \end{aligned}
$$
因此我们证明了任何一个率失真编码得到的率失真函数都不可能比信息论上的率失真函数来得更小。
率失真编码的存在性
对于存在性的证明,是依照这样的想法进行的:
设$X_1,X_2,…,X_n$是服从$p(x)$的独立同分布随机变量
设$d(x,\hat x)$为有界的失真度量
对于任何$D$,有$R \ge R^{(I)}(D)$
现在我们要证明的是,存在一组率失真编码,他们的码率都是$R$,而失真渐进达到$D$
这个过程与信道编码定理是很类似的,不同的是多了一个失真的约束。因此我们首先定义”失真”典型序列。
失真典型序列
设$p(x,\hat x)$和$d(x,\hat x)$分别是$X\times \hat X$上的联合概率分布和失真度量。对于任意$\epsilon>0$,若一个序列对$(x^n,\hat x^n)$满足以下条件,就被称为失真$\epsilon$-典型序列。
$$
\left. \begin{matrix} \lvert -\frac 1 n \log p(x^n) - H(X) \rvert < \epsilon\ \lvert -\frac 1 n \log p(\hat x^n) - H(\hat X) \rvert < \epsilon\ \lvert -\frac 1 n \log p(x^n,\hat x^n) - H(X,\hat X) \rvert < \epsilon\ \lvert d(x^n,\hat x^n) - E[d(X,\hat X)] \rvert < \epsilon \end{matrix} \right } $$
联合典型序列
前三个条件实际上就是联合典型序列的定义。实际上这个定义就是联合典型序列的拓展,失真联合典型序列一定是联合典型序列。
有了上面的定义,有这样一条引理:设$(X_i,\hat X_i)$是服从联合概率分布$p(x,\hat x)$的独立同分布随机变量,当$n\rightarrow \infty$时,$Pr(A_ {d,\epsilon}^(n)) \rightarrow 1$。
证明如下:
按照大数定理,前三个不等式的左侧都散以概率1收敛到期望值0的,而对于最后一个条件,我们有:
$$
d(x^n,\hat x^n) = \frac 1 n \sum_ {i=1}^n d(x_i,\hat x_i)
$$
根据大数定律,上式也会收敛到失真度量的统计平均。因此,最后一个条件也依概率1收敛到0。因此这个命题是成立的。
证明思路
与之前的香农第二定理一样,这里我们依然要用到随机生成的码本。
随机生成一个码本$C$,含有$2^{nR}$个序列$\hat X ^n \sim \prod _ {i=1}^n p(\hat x_i)$
将上述随机生成的$2^{nR}$个码进行编号$w \in {1,2,…,2^{nR} }$,因此我们可以确定的是这个信道的传输码率是$R$。
构造编码映射:
若$(X^n,\hat X^n(W)) \in A_ {d,\epsilon}^{(n)}$,则编码映射$X^n \rightarrow w$;若满足以上条件的$w$多于1,则取最小的$w$,否则,取$w = 1$。
构造解码映射:取恢复点为$\hat X^n (w)$
我们需要证明它的失真渐进等于$D$
这个信道的输入只有$2^{nR}$种字符,因此它的码率一定是$n$。
这个信道如图:

传输过程会有两种情况:
$\exists w$, \text{s.t. }$(x^n,\hat X^n(w)) \in A_ {d,\epsilon}^{(n)}$,则$d(x^n,\hat X^n(w)) < D+\epsilon$
不存在上述$w$,那么这时候$d(x^n,\hat X^n(w)) < d_ {max}$
因此得到:
$$
E[d(X^n,\hat X^n(X^n))] \leq (1-P_e)(D+\epsilon) + P_e \cdot d_ {max}\leq D + \epsilon +P_e \cdot d_ {max}
$$
为了证明,我们再引入两个数学引理:
- 对于所有$(x^n,\hat x ^n) \in A_ {d,\epsilon}^{(n)}$, p(\hat x^n) \ge p(\hat x^n| x^n) 2 ^{-n(I(X;\hat X)+3\epsilon)}
- 对于$0\leq x,y\leq 1,n>0$, (1 - xy)^n \leq 1 -x + e^{-yn}
再引入一个标记函数:
$$
k(x^n,\hat x^n) = \left { \begin{matrix} 1 & (x^n,\hat x^n )\in A_ {d,\epsilon}^{(n)}\ 0 & \text{otherwise} \end{matrix} \right.
$$
则:
$$
\begin{aligned} P_e &= \sum_ {x^n}p(x^n)[1-\sum_ {\hat x^n} p(\hat x ^n)k(x^n,\hat x^n)]^{2^{nR} }\ &\leq \sum_ {x^n}p(x^n)[1-2^{-n(I(X;\hat X) + 3\epsilon)} \sum_ {\hat x^n}p(\hat x^n|x^n)k(x^n,\hat x^n)]^{2^{nR} }\ &\leq \sum_ {x^n}p(x^n)[1-p(\hat x^n|x^n)k(x^n,\hat x^n) + \exp(-2^{-n(I(X;\hat X) + 3\epsilon)} 2^{nR})]\ &\leq 1- \sum_ {x^n\hat x^n}p(x^n)p(\hat x^n|x^n)k(x^n,\hat x^n) + \exp(-2^{n(R - I(X;\hat X) - 3\epsilon)}) \end{aligned}
$$
为了让上式趋于0,我们需要让$R \ge I(X;\hat X)$。而上式实际上就是$R \ge R^{(I)}(D)$。因此我们证明了,只要$R \ge R^{(I)}(D)$,失真是可以无限渐进逼近于$D$的。
最后,形象化的解释如下:
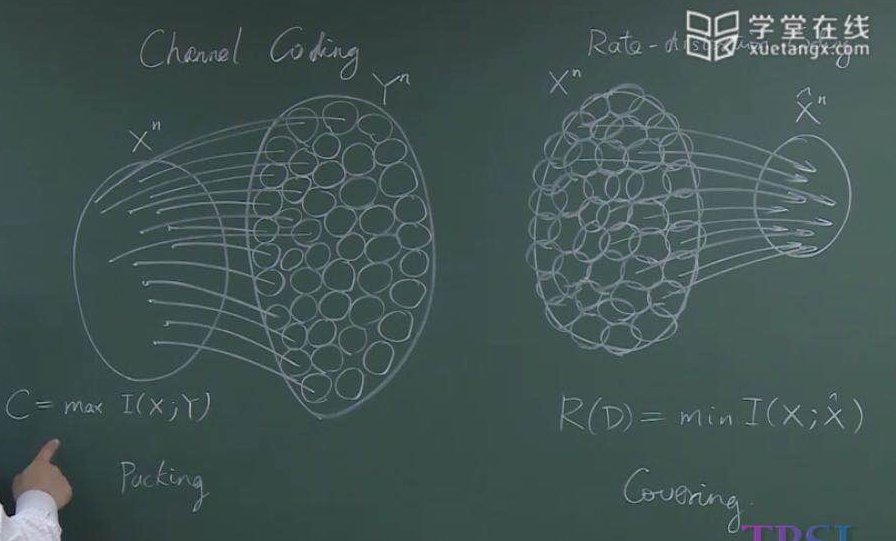
实际上推导到现在,我们也能够感觉到实际上信道编码定理和率失真定理之间是有一定的对偶关系的。在信道编码时候,由于信道噪声的存在,使得一个个$X^n$空间的点胀成了超球,而这个容量C就是最多能容纳多少个球。在率失真的情况下,由于失真$D$,我们想要求的是最少可以有多少个球可以覆盖信源。但是球的半径由于平均失真限制住,不能无限大。而这两个过程,正是对互信息的最大化和最小化。