信息论——信道及其容量(二)
到目前为止,我们都只算出来了信道容量,没有讲过怎么编码能得到这些容量。接下来要做的就是说明,所有上面算出来的容量,都是可以实现的。
一个信道如下图:
信道编码
这里我们先回忆一下之前的混乱打字机。之前说过,世界上任何一个数字信道,都可以直接或者间接地看作是混乱打字机模型。
对于信道${X,q(y|x),Y}$的信道编码包含以下要素:
- 输入符号集合${1,2,…,M}$
- 编码函数$X^n$:${1,2,…,M} \rightarrow X^n$,该函数为每一个输入符号产生了相应的信道编码码字$X^n(1),X^n(2),…,X^n(M)$,这些码字构成的集合称为“码本”。
- 解码函数$g$:$Y^n \rightarrow {1,2,…,M}$,该函数为一个确定性判决函数,将每一个可能的接受向量映射到一个输入符号。
意思也就是,对于符号个数为$M$的符号集,我们把它映射到一个长度为n的序列上,分n次传输。
信道编码的码率
$(M,n)$码的码率R定义为:
$$
R = \frac{\log M}{n} ,
$$
单位为比特/传输。这是信道码的每个码字母所能携带的最大的信息量。
如何理解?对于输入集合如果取等概分布,则它的信息量为$\log M$,这时候呢,$n$次传输才能传达这么多的信息量,所以每个传输的量就是$\frac{\log M}{n} = R$,则$M = 2^{nR}$。称这样的码为$(2^{nR},n)$码。
Example
重复码,输入字母数$M = 2$:${0,1}$,重复n次,这个码率为$1/n$。
直观来说,如果字符个数为$M$个,我们需要编码长度为$log M$就够了,这时候就可以保证码率为1。那为什么要进行这么复杂的定义?因为我们需要知道信道的传输是有噪声的。因此往往码率是要小于1,也就是n个长度本可以表示更大的字符集,但是我们选择它,增加码的冗余度,来降低错误率。比如下面的例子。
二进制奇偶校验码,输入字母数$M = 2^{n-1}:{x_1,x_2,…,x_ {n-1} }$,信道编码方案为$C = x_1,x_2,…,x_ {n-1}x_ {\text{parity} }$,其中$x_ {\text{parity} }$用于辨识码字中$1$的个数为奇数还是偶数,这个码率为:$\frac{n-1}{n}$。
信道编码的错误概率
输入为符号$i$时的条件错误概率为:
$$
\begin{aligned} \lambda_i &= Pr{g(Y^n) \ne i \vert X^n = x^n(i)}\ &= \sum_ {y^n} q(y^n\vert x^n(i))I(g(y^n) \ne i) \end{aligned}
$$
其中$I(\cdot)$为指示函数。
$(M,n)$码的最大错误概率为:
$$
\lambda^{(n)} = \max_ {i \in 1,2,…M} \lambda_i
$$
$(M,n)$码的算术平均错误概率为:
$$
P_e^{(n)} = \frac{1}{M} \sum_ {i=1}^M\lambda_i
$$
我们称一个码率$R$是可达的,若存在一个信道编码$(\lceil 2^{nR}\rceil,n )$,其最大差错概率在$n\rightarrow \infty$时趋于0。可以看出来可达要求无差错,而且是渐进的。
这时候我们得到信道容量的另外一个定义:一个信道的容量是该信道上所有可达码率的上确界,即$C = \text{sup }R$,这意味着$C$一定对应着一种信道编码方案。
经验主义式的设计
在信道传输中如何减少差错?由香农公式:
$$
C_T(\beta) = WT \log(1+\frac{P_S}{N_0W})
$$
可以得到,提高抗干扰能力的方法如下:
- 增加功率(提高信噪比)
- 加大带宽(信号变化剧烈)
- 延长时间(降低速率)
$C = max_ {p(x),功率约束}{I(X;Y)}$
而降低重复速率,实际上就是重复,增加冗余。
重复码
最直观的纠错方法就是:重复,增加冗余。
- 编码1:将每个输入元重复三次
- 纠正任一位上的错误
- 设码字记为$(c_8,c_7,…,c_0)$
- 由编码方法可知,信道无误时:$$ c_8 = c_7 = c_6\ c_5 = c_4 = c_3\ c_2 = c_1 = c_0$$
- 解码时,若$c_8 = c_6 \ne c_7$,则判定$c_7$位出错,采用简单多数法进行判定
- 依据是:连续出现两个错误的概率远远小于出现一个错误的概率
如下图,如果我们将上述编码放进二进制对称信道,则想要得到无差错编码。误码率的大小是重复$2n+1$次,而至少出现了$n+1$次错误。为了让误码率取0,$n \rightarrow 0$,此时码率也趋近于0,这不是一个好消息。
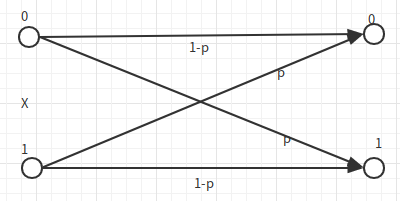
但是,是否对于信息的无差错传输,就意味着码率为0呢?答案是否定的。
现在我们考虑BSC信道,$W= {1,2,…,2^k}$,如下:
$$
W={1,2,…,2^k} \rightarrow \text{Encoder} \rightarrow X^n \rightarrow\text{BSC(p)} \rightarrow Y^n \rightarrow \text{Decoder} \rightarrow W
$$
我们可以得到:
$$
\begin{aligned} nC &\ge nI(X;Y)\ &\ge I(X^n;Y^n)\ &\ge I(W,\hat W)\ &=H(W) - H(W\vert \hat W)\ &\ge k - k H(P_e) \end{aligned}
$$
上式中最后一步是由Fano不等式得到的(不知道怎么得到,实际上我只能得到的是:$\ge k - (H(P_e)+kP_e)$)。
则:$$k \leq \frac{nC}{1 - H(P_e)}$$
而由于BSC信道的容量可以得到:$C = 1 - H(P)$,所以我们得到一个R的上界:
$$
R = \frac{k}{n} \ge \frac{1 - H(P)}{1 - H(P_e)}
$$
通过变形,我们可以得到:
$$
H(P_e) \ge 1 - \frac C R \rightarrow P_e \ge H^{-1}\left(1 - \frac C R\right)
$$
这意味着,如果想要让$P_e\leq 0$,则$R \leq C$,如果$R > C$,则$H(P_e)>0$,所以我们一定可以得到$P_e>0$,不可能进行可靠通信。
那么无差错传输的情况下,码率最大能有多少?先给你看一个preview,很直白的内容,不过它被证明确实是正确的:

想象信道将信源映射到一个球体里,而对每个输入符号也对应一个球。而这个球的体积就意味着噪声带来的体积,而大球中能容纳多少小球,正是这个信道编码在无错的情况下可以映射的符号数M。因为这个球的维度是n维的,我们可以得到:
$$
M = \frac{\left[\sqrt{P_S +P_N}\right]^n}{\left[\sqrt{P_N}\right]^n} = (1 + \frac{P_S}{P_N})^{\frac n 2}
$$
由上式,可以计算得出:
$$
R = \frac 1 2 \log (1 + \frac{P_S}{P_N})
$$
而这个值,正好与连续无记忆加性高斯噪声信道的容量一致。
当然,这个只是preview,不是严格的证明过程。下面对这个证明进行稍微严谨地推导,说明大多数噪声信道都有这样地特性。
为了证明这个东西,我们需要介绍一些别的定义。之前证明信源无失真压缩定理地时候,用到了典型序列,而这次我们在典型序列地基础上,重新介绍一个新的内容。
证明香农第二定理
联合典型序列
设$(X^n,Y^n)$是长为$n$的随机序列对,其概率分布满足
p(x^n,y^n) = \prod_ {i=1}^n p(x_i,y_i)
若$(X^n,Y^n)$满足以下条件,则称其为联合典型序列:
- $\lvert -\frac 1 n \log p(x^n) - H(X) \rvert < \epsilon$
- $\lvert -\frac 1 n \log p(y^n) - H(Y) \rvert < \epsilon$
- $\lvert -\frac 1 n \log p(x^n,y^n) - H(X,Y)\rvert < \epsilon$
联合典型序列构成的集合为$A_\epsilon^{(n)}$。
联合典型序列与之前典型序列定义是有很大地相似性:信息论——Lossless-Encoding。我们首先要看看联合典型序列的性质,才能用它来证明。
联合渐进等同分割定理(Joint AEP)
设$(X^n,Y^n)$是长度为$n$的随机序列对,其分布满足:
$$
p(x^n,y^n) = \prod_ {i=1}^n p(x_i,y_i)
$$
则以下性质成立:
- 当$n \rightarrow \infty$时,$Pr((X^n,Y^n) \in A_\epsilon ^{(n)}) \rightarrow 1$
- $(1 - \epsilon)2^{n(H(X,Y) - \epsilon)} \leq \vert A_\epsilon ^{(n)} \vert\leq 2^{n(H(X,Y)+\epsilon)}$
- 设$(\tilde{X^n},\tilde{Y^n})\sim p(x^n)p(y^n) $,即$\tilde{X^n},\tilde{Y^n}$统计独立,且具有与$p(x^n,y^n)$一致的边缘分布,则: $$Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \leq 2^{-n(I(X;Y) - 3\epsilon)}$$
若$n$足够大,则: $$Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \ge (1 - \epsilon)2^{-n(I(X;Y) + 3\epsilon)}$$
前两点都比较好理解,第三点中,$(\tilde{X^n},\tilde{Y^n})$是由$(X^n,Y^n)$的边缘分布依照$X^n,Y^n$独立形成的另一个联合分布,而这个分布属于典型序列的概率约等于$2^{-nI(X;Y)}$。
在这里我们证明以下第三条的前半部分:
$$
\tilde{X^n},\tilde{Y^n}\text{ are independent. }\tilde{X^n}\sim P_X(x^n),\tilde{Y^n}\sim P_Y(y^n)\ \begin{aligned} Pr{(\tilde{X^n},\tilde{Y^n}) \in A_\epsilon^{(n)} } &= \sum_ {(\tilde{x^n},\tilde{y^n}) \in A_\epsilon^{(n)} } P(x^n)P(y^n)\ &\leq 2^{b(H(X,Y) + \epsilon)}\cdot 2^{-n(H(X) - \epsilon)} \cdot 2^{-n(H(Y) - \epsilon)}\ &= 2^{-n(I(X;Y) - 3\epsilon)} \end{aligned}
$$
下图可以帮助我们更好地理解这些性质: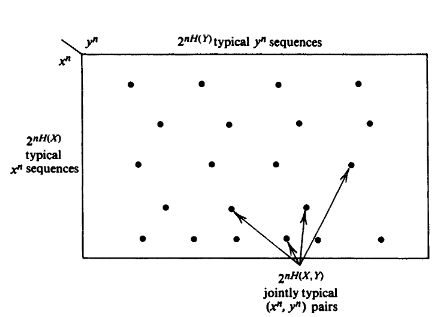
- 联合分布中,大约有$2^{nH(X)}$个典型X序列和$2^{nH(Y)}$个典型Y序列
- 其组合共有$2^{nH(X) + nH(Y)}$个,但是其中联合典型的只有$2^{nH(X,Y)}$个
- 随机选择而出现联合典型序列的概率为$2^{-nI(X;Y)}$
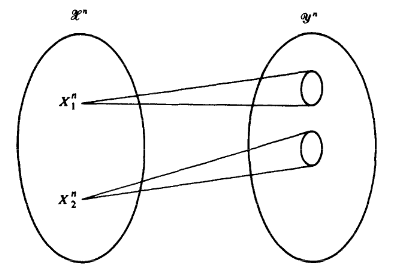
现在来看一下联合典型序列的另一个解释:
- 对于典型输入序列$x^n$,存在大约$2^{nH(Y|X)}$个可能的输出,且它们等概
- 所有可能的典型输出序列大约有$2^{nH(Y)}$个,这些序列被分成若干个不相交的子集
- 子集个数为$2^{n(H(Y) - H(Y|X))} = 2^{nI(X;Y)}$,表示信道可以无错误传递的最大字母序列个数
对于定理的证明包含两部分,一是可达性,也就是这个容量是可达的,第二个就是证明不可能达到比这个容量更好的速率。
可达性的证明
可达性的证明也就是我们可以找到一个编码函数和解码函数,使得信道带到容量C,而且是无差错地传输。
$$
W \in [1:2^{nR}] \rightarrow X^n \sim P_X(x) \rightarrow q(y|X)\rightarrow Y^n\rightarrow \hat W
$$
很反直觉的是,香农给我们编码方法是随机编码。这个随机编码指的是生成码字的过程为随机的:
$$
\text{Random Code:}\ \ell =\begin{pmatrix} x^n(1)\ x^n(2)\ \vdots\ x^n(2^{nR}) \end{pmatrix}
$$
其中$x^n(k)$是独立同分布的生成的,分布为$P_X(x^n(k)) = \prod_ {i=1}^n P_X(x_i(k))$
于是我们得到了码本,信源发送$x^n(k)$,而解码器收到$y^n$,一个长度为n的序列。
解码过程:如果解码器端找到唯一的$(x^n(\hat k), y^n) \in A_ {\epsilon}^{(n)}$,则解码得到$\hat k$。也就是$y^n$和一个唯一的$\hat k$对应的编码序列$x^n(\hat k)$属于联合典型序列,则解码为$\hat k$,否则解码出错。
现在我们分析一下出错概率。假设1为被传输的符号,而$y^n$为对应的输出。那么$x^n(1)$与$y^n$为联合典型序列的概率非常高。而另外一个i对应的$x^n(i)$与$y^n$为联合典型序列的概率就没有那么高了。实际上这个概率和联合典型序列性质的第三条是一致的。$x^n(i),y^n$有很大的概率是边缘典型序列,而随意两个边缘典型序列组合为联合典型序列的概率,正是
$$
Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \approx 2^{-nI(X;Y)}.
$$
出错的类型有两种。
- 传的是1,而没有联合典型,
- 传的是1,有多个和它是联合典型。
$$
\begin{aligned} P(E) &= P(E_1\cup E_2)\ &\leq P(E_1)+P(E_2)\ &\leq \epsilon + \sum_ {i=2}^{2nR}2^{-n(I(X;Y) - 3\epsilon)}\ &\leq \epsilon + 2^{3n\epsilon}2^{-n(I(X;Y) - R)} \end{aligned}
$$
我们希望$P(E) \rightarrow 0$,而第一项是可以任意小的,我们真正在意的是想要$I(X;Y)-R >0$。如果我们把生出随机码本的$P_X(x)$固定到$P^*_X(x)$,则$I(X;Y) = C$,于是只要$R<C$即可。
这个证明并不严谨,但是给我们提供了一个很重要的思维脉络。我们证明了$R < C$的情况下,可以实现无差错传输。
下面要说明的是定理的逆的证明。
converse证明
$$
\begin{aligned} nR &= H(W)\ &= H(W|\hat W) + I(W;\hat W)\ &= I(W;\hat W)\ &\leq I(X^n(W);Y^n)\ &= H(Y^n) - H(Y^n|X^n)\ &\leq \sum_ {i} H(Y_i) - \sum_ {i}H(Y_i|X_i)\ &= \sum_ {i} I(X_i;Y_i)\ &\leq nC \end{aligned}
$$
由此我们证明了,要想实现无差错的传输,那么$R\leq C$是一定成立的。由此香农第二定理的证明就结束了。和无差错编码一样,随机编码在现实中由于码本巨大也是难以实现的。不过在信息论提出的60年中,人类一次次提出新的编码,像香农界不断逼近。看着这些进步,感觉自己的信息论虽然没什么用到过,但是也没有白学。