Learning From Data——Reinforcement Learning
这周数据学习的内容是关于强化学习(Reinforcement Learning)的。不过课上睡着了,而且由于信息论时间太赶一直没有空看这节课的内容。
强化学习现在是非常流行的一个机器学习方法,当然它和其他的算法不一样,你用了这个就是这个,而强化学习更像是一种学习方式,也就是一直在线学习。AlphaGo赢了围棋冠军,OpenAI赢了Dota冠军,以及自动驾驶汽车飞机等都有它的身影。
什么是强化学习?
强化学习有点像是玩游戏的过程,实际上强化学习应用最多的地方也正是游戏。他属于无监督学习,但是又是根据奖励来决定下一个动作,怎么知道奖励?就是走到头。有点类似于有“长远的眼光”。这个长远的眼光可以说是经验,是通过一次次训练得到的,类似于你的人生可以来无数回,你会怎么做这件事。可能经过多次碰壁以后,我终于活成了一个成功人士。每次人生)训练周期)称为episode。
首先要知道对于序列决策问题,我们很难找到明确的监督策略来决定结果的好坏。在强化学习中,学习的过程是通过代理完成的。强化学习定义了一个奖励函数(reward function)和environment,而代理(agent)要做的就是最大化累计的奖励。如下图: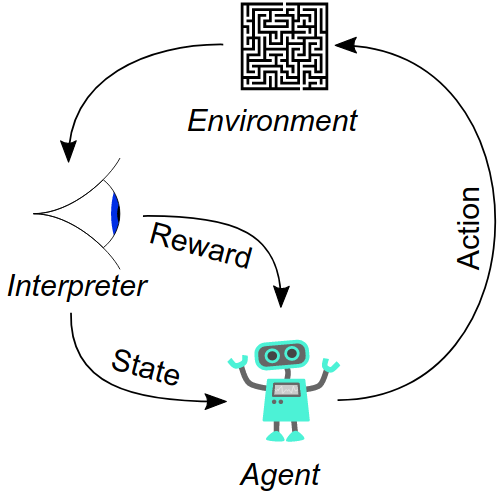
Markov Decision Process
我们首先学习一下马尔可夫决策过程。一个马尔可夫决策过程可以看作是一个五元组:$(S,A,{P_{sn} },\gamma,R)$,其中:
- $S$是一个状态集合(环境)
- $A$是一个动作集合
- $P_{sa}$是状态转移概率
- $R$:$S\times A \rightarrow \mathbb{R}$,是一个奖励函数
- $\gamma \in [0,1)$,为折扣因子(discount factor)

这幅图中,$S={S_0,S_1,S_2};A={a_0,a_1};R(s_1,a_0)=5,R(s_2,a_1) = -1$,而它的$P_{sa}$如下表:
|$S_0$|$S_1$|$S_2$
:–:|:–:|:–:|:–:|
$S_0,a_0$|0.5|0|0.5
$S_0,a_1$|0|0|1
$S_1,a_0$|0.7|0.1|0.2
$S_1,a_1$|0|0.95|0.05
$S_2,a_0$|0.4|0.6|0
$S_2,a_1$|0.3|0.3|0.4
现在考虑一个状态序列$S_0,S_1,…$以及对应的采取的动作$a_0,a_1,…,$
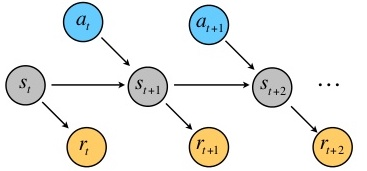
则这个序列的总共的奖励为:
$$
R(s_0,a_0) + \gamma R(s_1,a_1)+\gamma^2 R(s_2,a_2)+…
$$
我们把问题想得简单一点,假设这个reward只和状态有关,则总的奖励为:
$$
R(s_0)+\gamma R(s_1) + \gamma^2 R(s_2)+…
$$
未来第$t$步的奖励会被打$\gamma ^t$的折扣。这说明离当前这个状态越远权重越小,这意味着我们把下一步的奖励看得最重要,接下来是下下一步的奖励,依次减少。
Policy & Value functions
强化学习的目标就是:选择action,使得总的奖励期望最大:
$$
\mathbb{E}[R(s_0)+\gamma R(s_1) + \gamma^2 R(s_2)+…]
$$
- 一个策略(policy)是任意一个函数$\pi$:$S \rightarrow A$.
- 而该策略$\pi$对应的值函数(value function)为在从状态$s$开始,根据$\pi$来执行动作的条件下,总的奖励的期望值,也就是:
$$
V^\pi(s) = \mathbb{E}[R(s_0)+\gamma R(s_1) +\gamma^2 R(s_2) +…\vert s_0 = s,\pi]
$$
给定$\pi$,值函数(value function)满足Bellman等式:
$$
V^\pi(s)=R(s)+\gamma\sum_{s’ \in S}P_{s\pi(s)}(s’)V^\pi(s’)
$$
所以,这实际上是一个递归的过程,本次状态的值函数,是由下一个可能的状态值决定的。而下一个可能的状态值又和你的策略相关。为了方便理解,我们再定义一个函数,为动作-值函数Q。它接受两个输入:当前的状态$s$和当前状态采取的动作$a$:
$$
Q(s,a) = R(s)+\gamma\sum_{s’ \in S}P_{sa}(s’)V^\pi(s’)
$$
我们可以维护这一张关于Q值的表,这就是传说中的Q-learning。
Optimal value and policy
我们定义最优的值函数为:
$$
V^* (s) = \max_{\pi}V^\pi(s) = R(s)+\max_{a \in A}\gamma\sum_{s’ \in S}P_{sa}(s’)V^*(s’)
$$
最优的策略$\pi^*:S\rightarrow A$为实现了最优值函数的策略:
$$
\pi^*(s) = \arg\max_{a \in A}\sum_{s’\in S}P_{sa}(s’)V^ *(s’)
$$
对于每一个状态$s$以及每一个策略$\pi$,
$$
V^*(s) = V^{\pi *} \ge V^\pi(s)
$$
可以看到的是Q-learning是在维护一张表,而我们这里提到的和Q-learning非常相似,不过policy选的是最佳的动作,可以说Q-learning是实现这个目标学习的一种方法。
求解有限状态MDP下的最佳的value或者policy
实际上,我们可以看到只要解决了value和policy中一个,我们就能得到最佳的结果,因为实际上最佳策略也就是实现了最佳值的策略而已。因此这个解决过程就有两个方法。前提是,状态集合是有限的。
value iteration
假设MDP有有限的状态集合和动作空间,则值迭代如下:
1.For each state $s$ , initialize $V (s) := 0$
2.Repeat until convergence {
Update
$$V (s) := R(s) + \max_{a\in A} \gamma \sum_{s’ \in S} P_{sa} (s’)V(s’)$$
for every state s}
在这里有两个办法来更新$V(s)$:
- 同步更新(Synchronous update):
Set $V_0(s):= V(s)$ for all states $s \in S$
For each $s \in S$:
$$V(s):= R(s) + \max_{a \in A} \gamma \sum_{s’ \in S} P_{sa}(s’) V_0(s’)$$ - 非同步更新(Asynchronous update):
For each $s \in S$:
$$V(s):= R(s) + \max_{a \in A} \gamma \sum_{s’ \in S} P_{sa}(s’) V(s’)$$
policy iteration
1.Initialize $\pi$ randomly
2.Repeat until convergence{
a. Let $V:=V^\pi$
b. For each state $s$,
$$\pi(s):= \arg\max_{a \in A}\sum_{s’ \in S}P_{sa} V(s’)$$
}
其中步骤a可以通过求解Bellman等式来完成(一个$\vert S\vert$集合的线性方程组)。
Discussion
值迭代和策略迭代都可以最终收敛到最佳的$\pi^*$和$V^*$.
- 策略迭代对于小的MDP更加高效,可以更快速地收敛
- 值迭代对于更大的状态空间来说更实用
Learning a model for finite-state MDP
如果奖励函数$R(s)$和转移概率$P_{sa}$是未知的。如何从数据中估计他们?
Experience from MDP
给定政策$\pi$如下:
| $S$ | $\pi(s)$ |
|---|---|
| $s_0$ | $a_0$ |
| $s_1$ | $a_1$ |
| $s_2$ | $a_0$ |
在这个环境下重复地执行策略$\pi$:
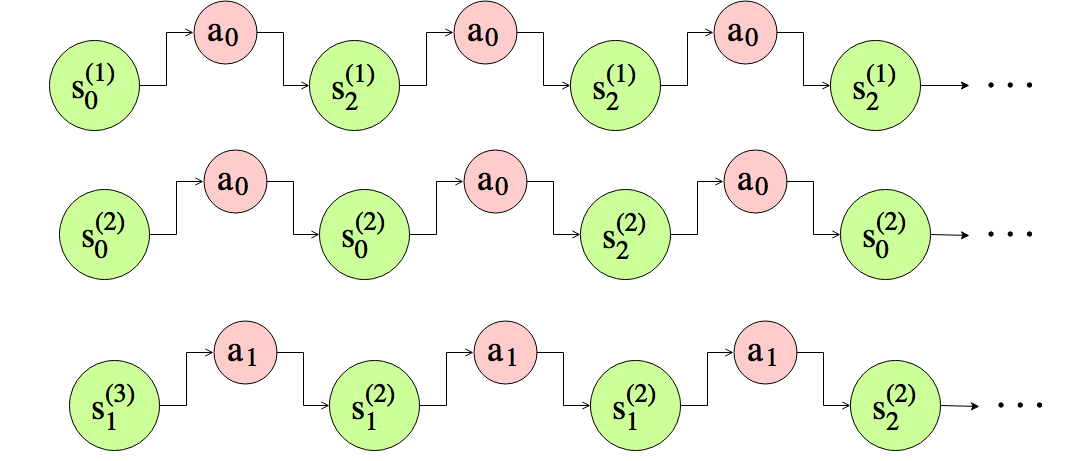
Estimate model from experience
Estimate $P_{sa}$
对状态转移概率的最大似然估计为:
$$
P_{sa}(s’) = P(s’|s,a)=\frac{\#{s \rightarrow a \rightarrow s’} }{\#{s \rightarrow a \rightarrow \cdot} }
$$
如果$\#{s \rightarrow a \rightarrow \cdot}=0$,那么设$P_{sa}(s’) = \frac{1}{\vert S\vert}$.
Estimate $R(s)$
我们定义$R(s)^{(t)}$为第t次试验中状态s的瞬时奖励,则:
$$
R(s) = \mathbb{E}[R(s)^{(t)}] = \frac{1}{m}\sum_{t=1}^mR(s)^{(t)}
$$
Algorithm: MDP model learning
1.Initialize $\pi$ randomly , $V (s) := 0$ for all $s$
2.Repeat until convergence {
a.Execute $\pi$ for $m$ trails
b.Update $P_{sa}$ and $R$ using the accumulated experience
c.$V:=$ValueIteration$(P_{sa},R,V)$
d.Update $\pi$ greedily with respect to $V$:
$$
\pi(s)= \arg\max_{a\in A}\sum_{s’\in S}P_{sa}(s’)V(s’)
$$
ValueIteration($P_{sa},R,V_0$)
1.Initialize $V = V_0$
2.Repeat until convergence{
Update
$$
V(s):=R(s)+\max_{a\in A}\gamma\sum_{s’\in S}P_{sa}(s’)V(s’)
$$
for every state s}
Continuous state MDPs
最后我们提一下连续的MDP,一个MDP的状态集合可能是无穷大的:
- A car’s state:$(x,y,\theta,\dot x,\dot y,\dot \theta)$
- A helicopter’s state:$(x,y,z,\phi,\theta,\psi,\dot x,\dot y,\dot z,\dot \phi,\dot \theta,\dot \psi)$
下面看一个有趣的例子:1D 倒立摆(Inverted Pendulum),目标是平衡车上的栏杆,如图:
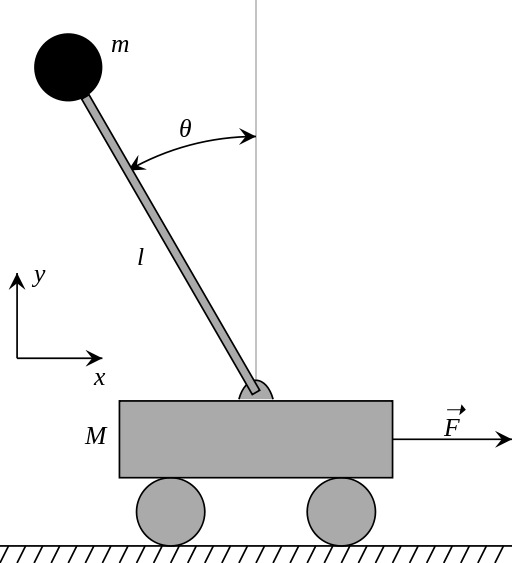
- 状态代表:$(x,\theta,\dot x, \dot\theta)$
- 动作:作用在车上的力$F$
- 奖励:每次这个栏杆是直立的时候+1
由于维度的“诅咒”,一般来说离散化只能在一维两维的情况下保持不错的效果。
如何直接估计$V$而不用离散化?
主要的想法:
- 获取MDP的模型或模拟器,可用于产生经验元组:$\langle s,a,s’,r \rangle$
- 现在有来自状态空间S的样本$s^{(1)},…,s^{(m)}$,使用模型来估计他们的最佳期望奖励总和,也就是:
$$
y^{(1)} \approx V(s^{(1)}),y^{(2)} \approx V(s^{(2)}),…
$$ - 使用监督学习从$\left(s^{(1)},y^{(1)}\right),\left(s^{(2)},y^{(2)}\right),…$来近似$V$,让其作为一个状态$s$的函数,例如:
$$
V(s)=\theta^T\phi(s)
$$
Obtaining a simulator
模拟器是一个黑盒子,在给定状态$s_t$和动作$a_t$的情况下来产生下一个状态$s_{t+1}$。
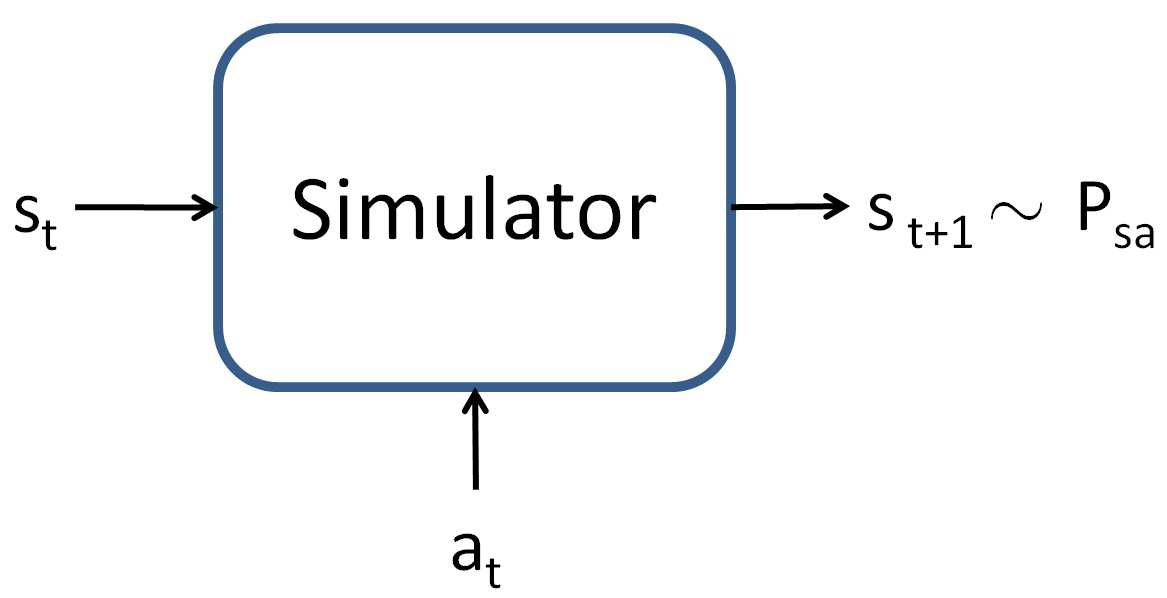
一般来说有下面几种策略:
- 使用物理法则,也就是倒立摆的运动方程:
$$
(M+m)\ddot{x}+b\dot{x} +ml\ddot \theta \cos(theta) - ml\dot \theta ^2\sin(\theta) = F\
(l+ml^2)\ddot\theta+mgl\sin(\theta) = -ml\ddot x\cos(\theta)
$$ - 使用现成的仿真软件
- 游戏模拟器
Obtaining a model
在MDP中我们重复地执行动作,执行m次试验,每个试验进行了T次。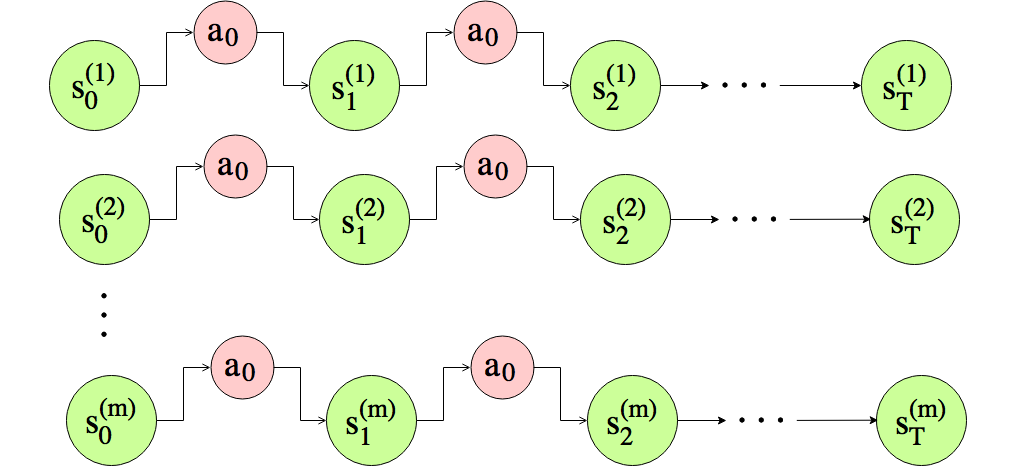
通过选择$\theta^*$来学习一个预测模型$s_{t+1}=h_\theta\left(\begin{bmatrix}s_t\a_t\end{bmatrix}\right)$,而:
$$
\theta^* = \arg\min_\theta\sum_{i=0}^m\sum_{t=0}^{T-1}\left\Vert
s_{t+1}^{(i)} - h_\theta \left(\begin{bmatrix}s_t\a_t\end{bmatrix}\right)
\right\Vert^2
$$
比较流行的预测模型有:
- 线性模型:$h_\theta = As_t+Ba_t$
- 带有特征映射的线性模型:$h_\theta = A\phi_s(s_t) + B\phi_a(a_t)$
- 神经网络
应用模型:
- 决策模型(Deterministic Model):$s_{t+1} = h_\theta \left(\begin{bmatrix}s_t\a_t\end{bmatrix}\right)$
- 随机模型(Stochastic Model):$s_{t+1} = h_\theta \left(\begin{bmatrix}s_t\a_t\end{bmatrix}\right)+\epsilon _t,\epsilon_t\sim \mathcal N (0,\Sigma)$
Value function approximation
如何直接近似$V$而不使用离散化?
主要的想法:
- 获得一个MDP的模型或者模拟器
- 现在有来自状态空间S的样本$s^{(1)},…,s^{(m)}$,使用模型来估计他们的最佳期望奖励总和,也就是:
$$
y^{(1)} \approx V(s^{(1)}),y^{(2)} \approx V(s^{(2)}),…
$$ - 使用监督学习从$\left(s^{(1)},y^{(1)}\right),\left(s^{(2)},y^{(2)}\right),…$来近似$V$,让其作为一个状态$s$的函数,例如:
$$
V(s)=\theta^T\phi(s)
$$
对于有限状态的MDP中,值函数的更新如下:
$$
V(s) := R(s)+\gamma \max_{a \in A}\sum_{s’ \in S}P_{sa}(s’)V(s’)
$$
而对于连续状态的值函数如下:
$$
\begin{aligned}
V(s) &:= R(s)+\gamma \max_{a \in A}\int_{s’}P_{sa}(s’)V(s’)ds’\
&:=R(s)+\gamma\max_{a\in A}\mathbb{E}{s’\sim P{sa} }[V(s’)]
\end{aligned}
$$
对于每个状态,我们使用有限的样本(来自$P_{sa}$)计算$y^{(i)}$来估计$R(s)+\gamma\max_{a\in A}\mathbb{E}{s’\sim P{sa} }[V(s’)]$.
Algorithm: Fitted value iteration(Stochastic Model)

Computing the optimal policy
在得到值函数的估计之后,对应的策略为:
$$
\pi (s) = \arg\max_{a}\mathbb{E}{s’\sim P{sa} }[V(s’)]
$$
根据经验来估计最优策略:
For each action $a$:
- Sample $s’_1,…,s’k \sim P{s,a}$ using a model
- Compute $Q(a) = \frac 1 k \sum_{j=1}^k R(s)+\gamma V(s’_j)$,$\pi(s) = \arg\max_aQ(a)$
除了线性回归,其他的学习算法也可以用来估计$V(s)$.