Learning From Data——Mixture of Gaussians & EM

这一周的内容是关于EM算法的，同时介绍了EM算法在混合高斯模型（Mixture of Gaussians）上的情况以及在因子分析上的用途。

首先介绍一下，什么是混合模型。

Mixture modes

一个混合模型假设数据是通过下面的过程生成的：

• 样本$z^{(i)} \in {1,…,k}$并且$z^{(i)}\sim Multinomial(\phi)$:$$p(z^{(i)} = j) = \phi_j \text{ for all }j$$
• 样本可以观测的量$x^{(i)}$是符合某些分布$p(z^{(i)},x^{(i)})$:$$p(z^{(i)},x^{(i)}) = p(z^{(i)})p(x^{(i)}\vert z^{(i)})$$

例如：非监督学习的手写识别是一个10个伯努利分布的混合模型，财务收益估计采用两个高斯混合模型，正态模型和危机时间分布。

而高斯混合模型为：
$$
z^{(i)}\sim Multinomial(\phi)\
x^{(i)} \sim \mathcal{N}(\mu_j,\Sigma_j)
$$

现在我们面临的问题是如何学习得到$\phi_j,\mu_j,\Sigma_j$？

这要分成两种情况来讨论：

• $z^{(j)}$是已知的，那么这个问题变成了一个监督学习的问题。解决的办法我们之前也学到过，实际上就是generative learning algorithm的一种，不过它实际上是二次判别分析的例子，比上面的博客的内容更稍微进了一步，可以看Covariance Matrix Derivation了解详情。在这个情况下：
  $$
  \phi_j = \frac{1}{m} \sum_{i=1}^m \mathbf{1}{z^{(i)} = j}, \mu_j = \frac{\sum_{i=1}^m \mathbf{1}{z^{(i)}=j}x^{(i)} }{\sum_{i=1}^m\mathbf{1}{z^{(i)} = j} }
  $$
  $$
  \begin{equation*}
  \begin{aligned}
  \Sigma_j = \frac{\sum_{i=1}^m \mathbf{1}{y_i=j}(x^{(i)} - \mu_{j}) (x^{(i)} - \mu_{j})^T}{\sum_{i=1}^m \mathbf{1}{y_i=j} }
  \end{aligned}
  \end{equation*}
  $$

• $z^{(j)}$是未知的，这时候则是属于非监督学习的范畴。我们使用期望最大化(expectation mamximization),也就是EM算法。

Expectation Maximization

EM算法是一个迭代求解最大似然估计的算法。求解最大似然估计我们已经遇到多次，与其他不同的地方在于，它估计的模型依赖于潜在的变量(latent variables)，这些变量是无法观察的。

首先，我们和往常一样，求数据的log-likelihood：
$$
I(\theta) = \sum_{i=1}^m\log p(x;\theta) = \sum_{i=1}^m\log\sum_z p(x,z;\theta)
$$

我们先来看看EM算法的步骤，然后再证明它的正确性：

Initialize θ

Repeat untill convergence {

(E - step ) For each i , set

$Q_i(z^{(i)} ):= p(z^{(i)} |x^{(i)} ; θ) \leftarrow $ Posterior distribution $z|x$ under $θ$

(M - step ) Set

$$\begin{equation}
\theta = \arg\max_{\theta} \sum_i \sum_{z^{(i)} }Q_i(z^{(i)}\log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})})
\end{equation}$$

$\leftarrow$ Update parameter θ
}

Proof of Correctness

我们将会证明(1)等价于$\arg\max_\theta I(\theta)$，也就是等式(1)是$I(\theta)$的一个很紧下界。我们也将会证明这个算法最终会收敛。
定义：
$$
J(Q,\theta) = \sum_j \sum_{z^{(i)} }Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}
$$
第一步：
我们要说明，$J(Q,\theta)$是$I(\theta)$的一个下界，而且当$Q_i(z^{(i)}) = p(z^{(i)}\vert x^{(i)};\theta)$时，这个下界是tight bound.

Jensen’s Inequality

首先需要回顾一下Jensen不等式。如果$f$是一个convex函数，若$X$为随机变量，则：
$$
\mathbf{E}[f(X)] \ge f(\mathbf{E}[X])
$$

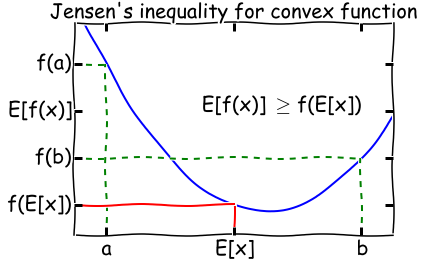
注意：

• 如果f(x)为concave函数，则$\mathbf{E}[f(X)] \leq f(\mathbf{E}[X])$.
• 如果f(x)为线性函数，则$\mathbf{E}[f(X)] = f(\mathbf{E}[X])$.

我们知道$\log$是一个concave函数，实际上，我们可以将$J(Q,\theta)$写为：
$$
\begin{aligned}
J(Q,\theta) &= \sum_j \sum_{z^{(i)} }Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\
&= \sum_j \mathbb{E}Q[log\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}] \
&leq \sum_j \log \mathbb{E}[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}]\
&= \sum_j \log \sum{z^{(i)} }Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\
&= \sum_j\log \sum_{z^{(i)} } p(x^{(i)},z^{(i)};\theta)\
&= I(\theta)
\end{aligned}
$$

如何证明是一个tight bound?

继续查看上面的Jensen不等式，想要这个不等式变得更紧一点，一个容易想到的策略是让$f$变为一个常量。因此在这里，最简单的做法就是让$\log$后的内容与$z^{(i)}无关$：
$$
\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} = C
$$

简单取$C=1$，我们得到：
$$
Q_i(z^{(i)}) = p(x^{(i)},z^{(i)};\theta)
$$

但是，因为$Q$是一个分布，因此我们必须要让$\sum_{z^{(i)} }Q_i(z^{(i)}) = 1$。所以$Q$的取值就比较容易求得了：
$$
\begin{aligned}
Q_i(z^{(i)}) &= \frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z^{(i)} }p(x^{(i)},z^{(i)};\theta)}\
&= \frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)});\theta}\
&= p(z^{(i)}\vert x^{(i)};\theta)
\end{aligned}
$$
因此，上面的推导同时也就证明了当$Q_i(z^{(i)}) = p(z^{(i)}\vert x^{(i)};\theta)$时，$J(Q,\theta)$是一个tight lower bound（取到了等号）。到这里，我们完成了E-step。

第二步，证明收敛。
EM算法会单调增加log-likelihood，也就是，如果$\theta^{(t)}$作为第ｔ次迭代的参数值，则：
$$
I(\theta^{(t)})\leq I(\theta^{(t+1)}),
$$
$$
Q_i^{(t)}(z^{(i)}) = p(z^{(i)}\vert x^{(i)};\theta^{(t)})
$$

这个证明和$Q$的取值息息相关。首先，从之前的推导，我们已经知道了：
$$
I(\theta ^{(t)}) = \sum_j \sum_{z^{(i)} }Q_i(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i(z^{(i)})}
$$

观察M-step，既然$\theta^{(t+1)}$是让上式取得最大值得到的$\theta$，那么可以得到：
$$
\begin{aligned}
I(\theta ^{(t+1)}) &\ge \sum_j \sum_{z^{(i)} }Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t+1)})}{Q_i(z^{(i)})}\
&\ge \sum_j \sum_{z^{(i)} }Q_i^{(t)}(z^{(i)})\log\frac{p(x^{(i)},z^{(i)};\theta^{(t)})}{Q_i(z^{(i)})}\
&= I(\theta^{(t)})
\end{aligned}
$$

第一步简单地由Jensen不等式得到（对于任何分布$Q$都是成立的）。由此我们便证明了这个算法最终会收敛。

EM for Mixture of Gaussians

现在我们来说明以下高斯混合模型下的EM算法。算法步骤如下：

Repeat until convergence{

(E - step ) For each i, j , set

$w^{(i)}_j:=p(z^{(i)} = j\vert x^{(i)};\phi,mu,\Sigma)$

(M - step ) Update parameters : assume $\phi_j = \mathbb{E}[w_j]$

$$\phi_j = \frac 1 m \sum_{i=1}^m w_j^{(i)};\
\mu_j = \frac{\sum_{i=1}^m w_j^{(i)}x^{(i)} }{\sum_{i=1}^mw_j^{(i)} };\
\Sigma_j = \frac{\sum_{i=1}^mw_j^{(i)}(x^{(i)} - \mu_j)(x^{(i)} - \mu_j)^T}{\sum_{i=1}^mw_j^{(i)} }
$$
}

下图是一个利用混合高斯模型EM算法的例子：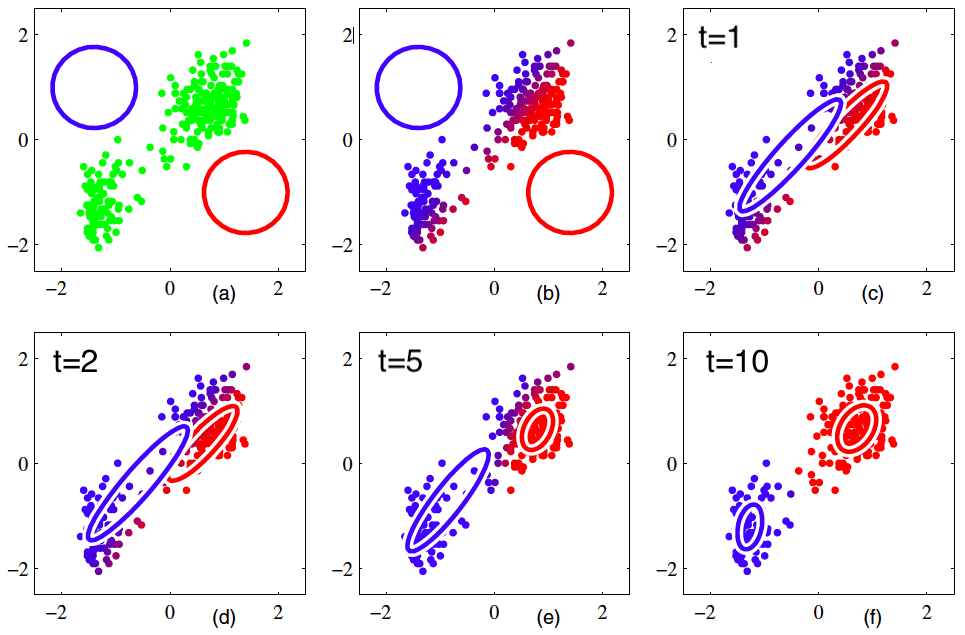

同时在这里我们可以看一下EM算法与Llyod’s k-means算法的比较：

可以看到，混合高斯模型可以看作是k-means聚类问题的一个“软”版本。

Factor Analysis

Example

Figure: Self-ratings on 32 Personality Traits

Figure: Pairwise correlation plot of 32 variables from 240 participants

Factor Analysis Terminology

首先介绍几个因子分析中的术语。

observed randam variables $x \in \mathbb{R}^n$
$$
x = \mu + Λz+\epsilon
$$

factor $z \in \mathbb{R}^{k}$ is the hidden (latent) construct that “causes” the observed variables.

factor loading $ Λ \in \mathbb{R}^{n\times k}$: the degree to which variable $x_i$ is “caused” by the factors.

$\mu,\epsilon \in \mathbb{R}^n$ are the mean and error vectors.

这一些解释我认为用中文翻译的有点别扭，所以就写成了英文。

下面是一个factor loading Λ的例子：

Table: Matrix of factor loading Λ for personality test data

variable	factor1	factor2	factor3	factor4
distant	0.59	0.27	0	0
talkative	-0.50	-0.51	0	0.27
careless	0.46	-0.47	0.11	0.14
hardworking	-0.46	0.33	-0.14	0.35
kind	-0.488	0.222	0	0
…	…	…	…	…

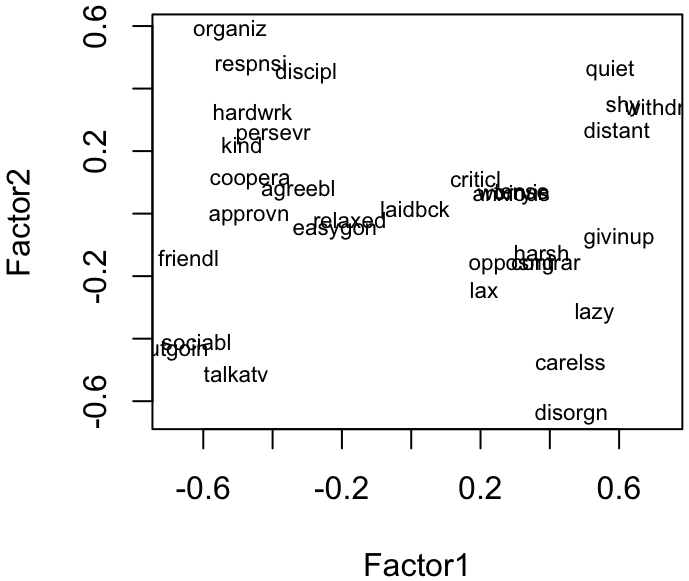
Figure: Visualize loading of the first two factors

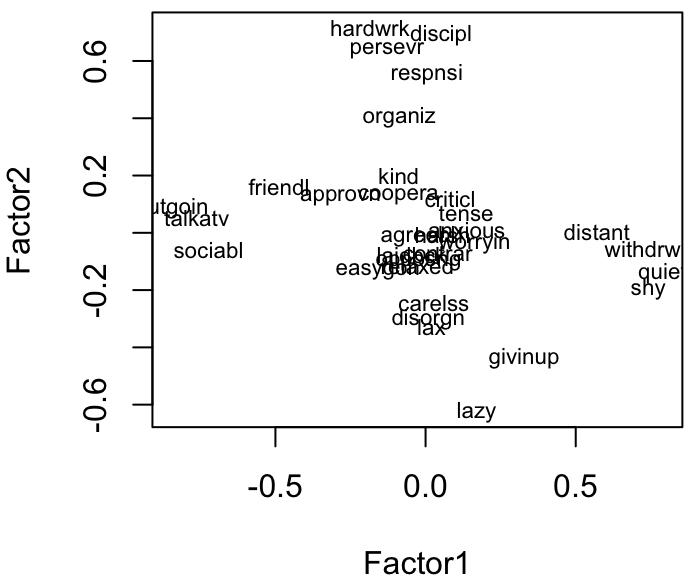
Figure: Visualize loading of the first two factors, rotated to align with axes

实际上因子分析也是一个混合模型，这里有可观察的变量：$x\in \mathbb R ^n$，以及潜在变量$z \in \mathbb{R}^k$，$(k < n)$.

因子分析模型定义了一个联合分布$p(x,z)$:
$$
z \sim \mathcal N(0,I)\
\epsilon \sim \mathcal N (0,\Psi)\
x = \mu + \wedge z + \epsilon
$$
其中$\Psi \in \mathbb{R}^{n \times n}$ 是一个对角矩阵，$\epsilon,\mu \in \mathbb R ^n$,并且互相独立, $\wedge \in \mathbb R ^{n \times k}$。

给定了$x^{(1)},…,x^{(m)}$，如何得到参数$\mu,\wedge,\Psi$？

EM for factor analysis

应该比较容易看出这个问题是可以用EM来解决的。下面写出迭代步骤：

Initialize µ,Λ,Ψ

Repeat untill convergence {

(E-step) For each i , set
$$
Q_i(z^{(i)}):= p(z^{(i)}\vert x^{(i)};\mu,\wedge,\Psi),
$$

z is a continuous variable

(M-step) Set

$$\begin{equation}
\mu,\wedge,\Psi:= \arg\max_{\mu,\wedge,\Psi} \sum_{i=1}^m\int_{z^{(i)} }Q_i(z^{(i)}) \log \frac{p(x^{(i)},z^{(i)};\mu,\wedge,\Psi)}{Q_i(z^{(i)})}dz^{(i)}
\end{equation}
$$

首先，我们需要把$p(z^{(i)}\vert x^{(i)}),p(z^{(i)},x^{(i)})$写成模型参数的形式。

我们的随机变量$\begin{bmatrix}z\x\end{bmatrix} \sim \mathcal N (\mu_{zx},\Sigma)$，其中：
$$
\mu_{xz} = \begin{bmatrix}
0\
\mu
\end{bmatrix},\Sigma = \begin{bmatrix}
I&\wedge^T\
\wedge&\wedge\wedge^T+\Psi
\end{bmatrix}
$$

我们知道 $\mathbb{E}[z] = 0$,因为$ z \sim \mathcal N(0,I)$。同时我们也可以得到：
$$
\begin{aligned}
\mathbb{E}[x]&=\mathbb{E}[\mu+\wedge z+\epsilon]\
&=\mu+\wedge\mathbb E [z]+\mathbb{E}[\epsilon]\
&=\mu
\end{aligned}
$$

所以可以得到：
$$
\mu_{xz} = \begin{bmatrix}
0\
\mu
\end{bmatrix}
$$

如果想要得到$\Sigma$，需要比较长的推导。如果不在乎的过程的话可以直接跳过。

$\Sigma$’s derivation

为了得到$\Sigma$，我们需要计算$\Sigma_{zz} = \mathbb{E}[(z − \mathbb{E}[z])(z − \mathbb{E}[z])^T]$($\Sigma$的左上角)，$\Sigma_{zx} = \mathbb{E}[(z − \mathbb{E}[z])(x − \mathbb{E}[x])^T]$($\Sigma$的右上角)以及$ \Sigma{xx} = \mathbb{E}[(x − \mathbb{E}[x])(x − \mathbb{E}[x])^T] $(右下角)。

首先，因为$z \sim \mathcal N(0,I)$，我们可以轻易得到：$\Sigma_{zz} = Cov(z) = I$。此外：
$$
\begin{aligned}
\mathbb{E}[(z − \mathbb{E}[z])(x − \mathbb{E}[x])^T] &= \mathbb{E}[z(\mu+\wedge z + \epsilon - \mu)^T]\
&= \mathbb{E}[zz^T]\wedge^T + \mathbb{E}[z\epsilon^T]\
&=\wedge^T
\end{aligned}
$$
在最后一步中，我们利用了$ \mathbb{E}[zz^T] = Cov(z)$，因为z是zero-mean，以及$ \mathbb{E}[z\epsilon^T] = \mathbb{E}[z] \mathbb{E}[\epsilon] = 0$，因为他们是独立的。最后:
$$
\begin{aligned}
\mathbb{E}[(x − \mathbb{E}[x])(x − \mathbb{E}[x])^T] &= \mathbb{E}[(\mu+\wedge z + \epsilon - \mu)(\mu+\wedge z + \epsilon - \mu)^T]\
&= \mathbb{E}[\wedge z z^T\wedge^T + \epsilon z^T \wedge^T + \wedge^T z \epsilon^T + \epsilon\epsilon^T]\
&=\wedge \mathbb{E}[zz^T]\wedge^T + \mathbb{E}[\epsilon\epsilon^T]\
&= \wedge\wedge^T+\Psi
\end{aligned}
$$

最后我们就得到了：
$$
\Sigma = \begin{bmatrix}
I&\wedge^T\
\wedge&\wedge\wedge^T+\Psi
\end{bmatrix}
$$

E-step

E-step不难理解，因为后验分布：$$z^{(i)}\vert x^{(i)} \sim \mathcal N \left( \mu_{z^{(i)}\vert x^{(i)} },\Sigma_{z^{(i)}\vert x^{(i)} }\right)$$，根据EM算法可以得到：
$$
\mu_{z^{(i)}\vert x^{(i)} } = \wedge^T(\wedge\wedge^T + \Psi)^{-1}(x^{(i)}-\mu)\
\Sigma_{z^{(i)}\vert x^{(i)} } = I - \wedge^T(\wedge\wedge^T + \Psi)^{-1}\wedge\
Q_i(z^{(i)}) = \frac{1}{(2\pi)^{k/2}\vert \Sigma_{z^{(i)}\vert x^{(i)} }\vert^{1/2} }\exp\left(-\frac{1}{2}(z^{(i)} - \mu_{z^{(i)}\vert x^{(i)} })^T\Sigma^{-1}{z^{(i)}\vert x^{(i)} }(z^{(i)} - \mu{z^{(i)}\vert x^{(i)} })\right)
$$

M-step

$$
\begin{equation}
\arg\max_{\mu,\wedge,\Psi} \sum_{i=1}^m\int_{z^{(i)} }Q_i(z^{(i)}) \log \frac{p(x^{(i)},z^{(i)};\mu,\wedge,\Psi)}{Q_i(z^{(i)})}dz^{(i)}
\end{equation}
$$

我们可以知道：
$$
\int_{z^{(i)} }Q_i(z^{(i)}) \log \frac{p(x^{(i)},z^{(i)};\mu,\wedge,\Psi)}{Q_i(z^{(i)})}dz^{(i)} \
=\mathbb{E}{z\sim Q_i}[\log p(x^{(i)}|z^{(i)};\mu,\wedge,\Psi) + \log p(z^{(i)})−\log Q_i(z^{(i)})]
$$
所以(3)也就等价于：
$$
\begin{equation}
\arg\max{\mu,\wedge,\Psi} \sum_{i=1}^m\mathbb{E}_{z\sim Q_i}[\log p(x^{(i)}|z^{(i)};\mu,\wedge,\Psi) + \log p(z^{(i)})−\log Q_i(z^{(i)})]
\end{equation}
$$

因为$x =\mu + \wedge z + \epsilon,\epsilon \sim \mathcal N (0,\Psi)$，我们可以得到：
$$
x^{(i)}\vert z^{(i)} \sim \mathcal N (\mu+\wedge z,\Psi)
$$
即：
$$
p(x^{(i)}|z^{(i)};\mu,\wedge,\Psi)\
=\frac{1}{(2\pi)^{n/2}\vert \Psi\vert^{1/2} }\exp\left(-\frac{1}{2}(x^{(i)} - \mu-\wedge z^{(i)})^T\Psi^{-1}(x^{(i)} - \mu-\wedge z^{(i)})\right)
$$

我们通过$\mu,\wedge,\Psi$来最大化(4)。

与混合高斯模型的对比

• 混合高斯模型假设有足够的数据和相对较少的随机变量，也就是当$n\approx m$或者$n > m$，$\Sigma$是奇异矩阵。
• 而因子分析在$n > m$的时候通过允许模型误差来处理。

与PCA的关系

• 他们都能找到低纬度潜在的子空间。
• PCA可以用来做数据压缩，或者去除冗余数据，它减少了可以观察的数据间的联系。
• 因子分析适合来做数据勘探，来找到观测数据中的独立，共同因子。
• 因子分析允许噪声具有任意的对角协方差矩阵，而PCA假设噪声是球形的。

总之，这节课上的还是很懵逼的。

参考资料：
EM algorithm，factor analysis