Learning From Data——Kernel PCA
上次说了几个PCA的局限性,其中有一个是它只找各个特征之间的线性关系。如何拓展线性关系到非线性,似乎有点思路,因为之前SVM中说过,可以通过kernel将SVM拓展到非线性的分类。同样通过kernel,我们也可以找到特征之间的非线性关系,从而利用PCA进行数据压缩等操作。
对于线性的PCA的扩展,就是将PCA映射到更高维度的空间,使其在更高维度的空间有线性关系:$\phi:\mathbb{R}^n \rightarrow \mathbb{R}^d,d\ge n$.而如何映射,通过一个kernel函数来定义:$k(X_i,X_j) = \phi(X_i)^T\phi(X_j)$或者kernel矩阵$K \in \mathbb{R}^{m \times m}$. 映射完成后,我们就可以在更高维度的空间再使用标准的PCA算法了。不过这个想法是naive的,比如高斯核函数,是映射到无限维度,如果用原来的PCA去求,是不现实的。而且,从下面的分析可以看到,直接求也用不到kernel函数的方便之处。
映射后的数据的协方差矩阵如下:
$$
\Sigma = \frac 1 m \sum_ {i=1}^m \phi(X_i) \phi(X_i)^T \in \mathbb{R}^{d\times d}
$$
假如$(\lambda_k,v_k),k=1,…,d$为$\sigma$的特征分解,则:
$$
\Sigma v_k = \lambda_k v_k
$$
则原来$X_l$的在第k个主要成分的投影为:$\phi(X_l)^Tv_k$.
到目前位置,我们都没有用到kernel。$\phi(X_i)$是难以计算的,而kernel是容易计算的。因此如何避免$\phi_(X_i)$的计算?
首先我们知道:
$$
\begin{align}
\Sigma v_k = \left (\sum_ {i=1}^m \phi(X_i) \phi(X_i)^T \right ) v_k = \lambda _k v_k
\end{align}
$$
实际上,我们可以将$v_k$写成$\phi(X_i)^T$的组合(这个很像是之前的kernel logistic regression用的trick),这里就不证明为什么一定可以写成这个组合了,我觉得应该会用到线性代数的秩的知识。
$$
v_k = \sum_ {i = 1} ^m \alpha_i^{(k)} \phi(X_i)
$$
那么,之前提到的投影可以将上式带入:
$$
\begin{aligned}
\phi(X_l)^Tv_k &= \phi(X_l)^T \sum_ {i = 1} ^m \alpha_i^{(k)} \phi(X_i)\
&= \sum_ {i=1} ^m \alpha_i^{(k)} \phi(X_l)^T\phi(X_i)\
&= \sum_ {i=1} ^m \alpha_i^{(k)} k(X_l,X_i)
\end{aligned}
$$
这又引入了一个问题:如何得到$\alpha_i^{(k)}$?
将$v_k = \sum_ {i = 1} ^m \alpha_i^{(k)} \phi(X_i)$带入(1)式,我们得到:
$$
\left[\sum_ {i=1}^m \phi(X_i) \phi(X_i)^T \right] \left(\sum_ {i=1}^m \alpha_i^{(k)} \phi(X_i) \right) = \lambda_k m \left(\sum_ {i=1}^m \alpha_i^{(k)} \phi(X_i) \right)\
\Phi(X)^T \Phi(X) \Phi(X)^T \alpha^{(k)} = \lambda_k m \Phi(X)^T \alpha^{(k)}\
\Phi(X) \Phi(X)^T \alpha^{(k)} = \lambda_k m \alpha^{(k)}\
K \alpha^{(k)} = \lambda_k m \alpha_k,
$$
上式中:
$$
\alpha ^{(k)} = \begin{bmatrix}
a_1^{(k)}\
\vdots\
a_m^{(k)}
\end{bmatrix};\Phi(X) = \begin{bmatrix}
\phi(X_1)^T\
\vdots\
\phi(X_m)^T
\end{bmatrix} \
K = \begin{bmatrix}
k(X_1,X_1)&k(X_1,X_2)&\cdots&k(X_1,X_m)\
k(X_2,X_1)&k(X_2,X_2)&\cdots&k(X_2,X_m)\
\vdots&\vdots\ &\ddots&\vdots\
k(X_m,X_1)&k(X_m,X_2)&\cdots&k(X_m,X_m)
\end{bmatrix}
$$
上式中$\alpha^{(k)}$可以通过求解K的特征向量得到,而K是kernel矩阵。
我们希望正交化$\alpha^{(k)}$,使得$v_k^Tv_k = 1$(与之前的标准PCA一致).
$$
v_k^T v_k = (\alpha^{(k)})^T \Phi(X) \Phi(X)^T \alpha^{(k)} = \lambda_k m ((\alpha^{(k)})^T \alpha^{(k)}).
$$
所以$\Vert \alpha^{(k)} \Vert^2 = \frac{1}{\lambda_k m} $.
此外,如果$\mathbb{E}(\phi(X)) \ne 0$,我们还需要中心化$\phi(X)$:
$$
\tilde{\phi}(X_i) = \phi(X_i) - \frac 1 m \sum_ {l=1}^m \phi(X_i)
$$
而中心化以后的kernel矩阵为:
$$
\tilde{k}(i,j) = \tilde{\phi}(X_i)^T \tilde{\phi}(X_j)
$$
写成矩阵就是:
$$
\tilde{K} = K -1_m K - K 1_m + 1_mK1_m
$$
其中:
$$
1_m = \begin{bmatrix}
\frac 1 m & \cdots &\frac 1 m\
\vdots & \ddots & \vdots\
\frac 1 m & \cdots &\frac 1 m
\end{bmatrix} \in \mathbb{R}^{m\times m}
$$
我们从前面已经推导出来,计算kernel PCA的$v_k$最终需要的是kernel矩阵,因此使用$\tilde{K}$去计算PCA即可。
2个问题:
- 之前的X不光是中心化的,而且还是Stdev(X) = 1,在kernel PCA中没有考虑这一点吗?
对于kernel PCA的标准协方差分析是非常困难的。不过协方差的意义在于使得数据范围不会变动过大(如身高m为单位,变化程度可能是1以内,而体重以斤为单位,变化范围为几十),因此如果对原数据进行协方差变0的操作后,假设kernel是对称的,它们的变化范围不会差得过多。
- $a^{(k)}$算出来有m个,但是我们不一定把它映射到m维度的空间了。不像原来的PCA,n维有n个特征向量?
一般来说我们升维时候都会升到无限维度,很少有比m小的。这时候它的特征向量个数就受到了数据个数的限制。如果维度比m小,则特征向量不会真正达到m个。
总结以下,kernel PCA的步骤:
求出K
求出$\tilde{K}$
求出上面的特征值和特征向量,并且根据使得特征向量的长度等于$\frac {1}{\sqrt{\lambda_k m} }$,其中$\lambda_km$也就是对应的特征值。
根据求得的特征向量,求得$v_k$.
Kernel PCA的例子:
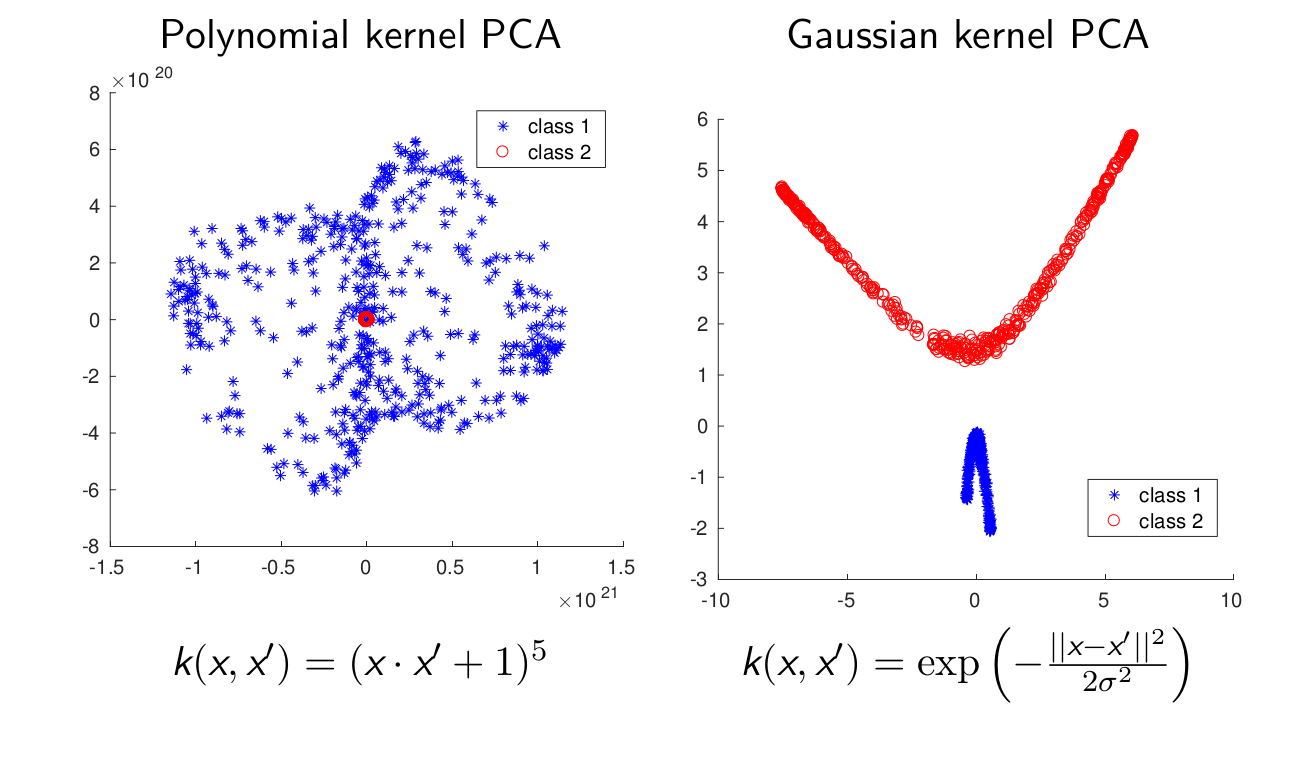
kernel PCA经常用于聚类,异常检测等等。它需要找到$m \times m$的特征向量来代替$n \times n$。通过投影到k维主子空间进行降维通常是不可能的,也就是一般不用kernel PCA来进行数据压缩。