Learning From Data——K-Means Clustering
转眼间这一个学期已经过了一半了。开始学习非监督学习算法了。第一个介绍的算法,是K-Means聚类算法。
这是第一篇讲unsupervised learning的算法,先说一下,unsupervised learning试图在做些什么。
非监督学习和监督学习很像,都是希望学习出一个模型,$x \rightarrow f(x)$。不过非监督没有标签了。所以一般来说非监督学习更难。
非监督学习的目标,是想找到输入特征X的代表(Representation)。Representation learning problem可以描述为:给定了输入X,找到更简单的特征Z来保存和X一样的信息。
说了这么多,这哪像是一个学习算法,这更像是压缩算法。实际上,非监督学习就广泛应用于压缩。
一般,好的representation有以下几个特点:
低维度:把信息压缩得更小
稀疏代表:比如一个矩阵,大部分项都是0,可以大大简化计算,称为稀疏矩阵。而稀疏代表也即大部分数据的特征的大部分项都是0.
独立代表:disentangle the source of variations.这个翻译是解开变异之源……好中二的感觉。这个是什么意思我也不是很理解。
非监督学习广泛用于数据压缩,异常检测,分类聚类等等。
而这次要说的算法:K-Means算法,是一个聚类算法。
聚类的目标是给定一组输入特征,将数据分成几组结合在一起的簇。
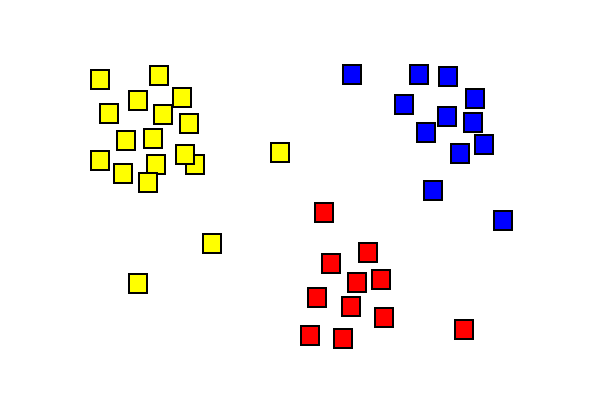
聚类的理想结果应满足下面的条件:
- 在同一个簇中的对象相比于不同的簇的对象来说更为相似。
K-Means问题描述
给定n个样本:${X_1,X_2,…,X_n}$,将它们分为k个类($k\leq n$)$C_1,C_2,…,C_k$,使得簇内平方和(within-cluster sum of squares,WCSS)达到最小:
$$
argmin_C \sum_ {j=1}^k \sum{x \in C_j} \Vert x - \mu_j \Vert ^2
$$
$\mu_j$是一个簇的中心:$\mu_j =\frac{1}{ \vert C_j \vert } \sum_ {X \in C_j} X_j$。
这个问题还有其他几种等价的描述:
最小化簇内协方差:$\sum_ {j=1}^k \vert C_j\vert Var(C_j)$
最小化相同的簇内点的两两平方偏差:$\sum_ {i=1}^k \frac 1 {2\vert C_i \vert} \sum_ {x,x’\in C_i} \Vert x - x’ \Vert$
最大化簇与簇之间的平方和(BCSS)
在欧几里得空间找到最好的聚类效果(全局最优解)是一个NP-hard问题。因此经常用启发式,迭代式的算法来得到聚类效果,一般得到的是局部最优解。
Llyod’s Algorithm
虽然全局最优解是一个NP-hard问题,但是得到局部最优解确实非常容易的。在这里介绍Llyod’s Algorithm, 实际上它的过程是异常简单的。整个算法分为下面几步:
随机初始化k个中心:$u_1,u_2,…,u_k$
对于每个样本i,$C^{(i)} = argmin_j \Vert X_i - \mu_j \Vert^2$
根据聚类结果重新计算$\mu_j$
重复上述过程,直到$\mu$不再改变。
现在,从非监督学习的目标来重新理解这个聚类算法,它实际上是学习到了一个k-dimentional的稀疏代表。也就是:$X_i$转换到$Z_i$了,而
$z_ {i,j} =\left { \begin{matrix}
1& if C^{i} = j;\
0& otherwise
\end{matrix}
\right .
$
它将原来的X特征向量转换成Z维向量。而这个Z矩阵是稀疏的,因为每个向量只有一项值为0.
因为这个算法只能得到一个局部最优解,因此初始化是很重要的,可能会影响结果。
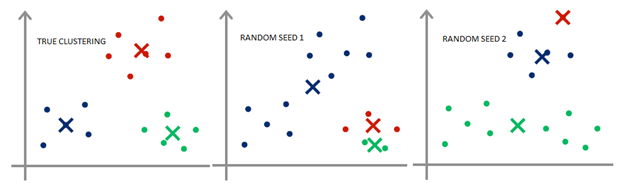
这个算法还留下几个疑问:
- 如何初始化?
Uniformly random sampling,
kmeans++ [Arthur & Vassilvitskii SODA 2007]: distance-based sampling
- 如何自动选择分成几类(k的取值)?
Cross validation(交叉验证)
G-Means [Hamerly & Elkan, NIPS 2003]
说到最后,说几句题外话。数据学习进行了期中考试,我的分数是后30%的水平。我的心里还是挺难过的。虽然我的本科也是很差的排名,但是那是因为我不学习。不过数据学习这门课我学得还是挺认真的。
我可以给自己找很多借口:没有复习;时间没安排好(第一题花了太长时间)等等,不过主要原因还是实力不够。就算这些我都做到了,我依然及不了格。既然有80分的大佬,那在乎这几分也没什么意思。说明自己还是太菜了。
希望期末考试可以取得一个好成绩。