Learning From Data——拟合sin曲线

Posted on Edited on In

这次的作业是用神经网络来拟合sin曲线。通过实践更能感受到ReLU以及sigmoid，tanh激活函数的区别。

作业中已经将整体框架写好，好让我们能专注于算法部分。比较复杂的部分是向量化，因为自己的博客定义的这个矩阵的形式可能是多样的，但是最后的结果肯定是一致的，以及需要传入的参数如何分配。

我选择传入的input为$a^{(l)}$以及$a^{(l-1)}$，传入的gran_out为$\sigma^{(l)}$中除去乘$g’(z)$的部分。因为导数部分需要上一层的激活函数来决定。

在作业中定义W,a的方式和我定义$\Sigma,a$的方式正好相反，这是需要注意的地方。

这个神经网络包含4层：输入层，全连接层（1×80），ReLU层（80×80），输出层（80×1）。

最后得到的拟合结果和loss曲线如下：

purelin:

loss history:

tanh:

loss history:

代码会在作业截止后上传。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('ggplot') 
  

x = np.linspace(-np.pi,np.pi,140).reshape(140,-1)
y = np.sin(x)
lr = 0.02     #set learning rate

def sigmoid(x):
    return 1/(np.ones_like(x)+np.exp(-x))
def tanh(x):
    return (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))

def mean_square_loss(y_pre,y_true):         #define loss 
    loss = np.power(y_pre - y_true, 2).mean()*0.5
    loss_grad = (y_pre-y_true)/y_pre.shape[0]
    return loss , loss_grad           # return loss and loss_grad
    
class ReLU():                     # ReLu layer
    def __init__(self):
        pass
    def forward(self,input):
        unit_num = input.shape[1]
        # check if the ReLU is initialized.
        if not hasattr(self, 'W'):
            self.W = np.random.randn(unit_num,unit_num)*1e-2 
            self.b = np.zeros((1,unit_num))
        temp = input.dot(self.W) + self.b.repeat(input.shape[0]).reshape(self.W.shape[1],input.shape[0]).T
        return np.where(temp>0,temp,0)
        
    def backward(self,input,grad_out):
        a_lm1 = input[0]
        a_l = input[1]
        derivative = np.where(a_l>0,1,0)
        sample_num = a_lm1.shape[0]
        delt_W =  a_lm1.T.dot(grad_out*derivative)/sample_num
        delt_b = np.ones((1,sample_num)).dot(grad_out*derivative)/sample_num
        to_back = (grad_out*derivative).dot(self.W.T)
        self.W -= lr * delt_W
        self.b -= lr * delt_b
        return to_back
        
        

class FC():
    def __init__(self,input_dim,output_dim):    # initilize weights
        self.W = np.random.randn(input_dim,output_dim)*1e-2 
        self.b = np.zeros((1,output_dim))
                       
    def forward(self,input):          

        #purelin
        #return input.dot(self.W) + self.b.repeat(input.shape[0]).reshape(self.W.shape[1],input.shape[0]).T
        #tanh
        return tanh(input.dot(self.W) + self.b.repeat(input.shape[0]).reshape(self.W.shape[1],input.shape[0]).T)
        
        
    # backpropagation,update weights in this step
    def backward(self,input,grad_out):
        a_lm1 = input[0]
        a_l = input[1]
        sample_num = a_lm1.shape[0]
        #purelin
        '''delt_W =  a_lm1.T.dot(grad_out)/sample_num
        delt_b = np.ones((1,sample_num)).dot(grad_out)/sample_num
        to_back = grad_out.dot(self.W.T)'''
        #tanh
        delt_W =  a_lm1.T.dot(grad_out*(1-np.power(a_l,2)))/sample_num
        delt_b = np.ones((1,sample_num)).dot(grad_out*(1-np.power(a_l,2)))/sample_num
        to_back = (grad_out*(1-np.power(a_l,2))).dot(self.W.T)
        self.W -= lr * delt_W
        self.b -= lr * delt_b
        return to_back

#  bulid the network      
layer1 = FC(1,80)
ac1 = ReLU()
out_layer = FC(80,1)

# count steps and save loss history
loss = 1
step = 0
l= []

while loss >= 1e-4 and step < 15000: # training 
            
    # forward     input x , through the network and get y_pre and loss_grad   
    # To get a[l]
    a = [x]
    a.append(layer1.forward(a[0]))
    a.append(ac1.forward(a[1]))
    a.append(out_layer.forward(a[2]))
    #backward   # backpropagation , update weights through loss_grad
    #sigma and a[l-1] is what the backpropagation needs. If you want get the derivative, the a[l] is also needed.  
    sigma = out_layer.backward([a[2],a[3]],a[3] - y)
    sigma = ac1.backward([a[1],a[2]],sigma)
    sigma = layer1.backward([a[0],a[1]],sigma)    
    #This step is for plotting the initial line.
    if step == 0:
        y_start = a[3]
    step += 1
    loss = mean_square_loss(a[3],y)[0]
    
    l.append(loss)
    #print("step:",step,loss)
y_pre = a[3]
    
# after training , plot the results

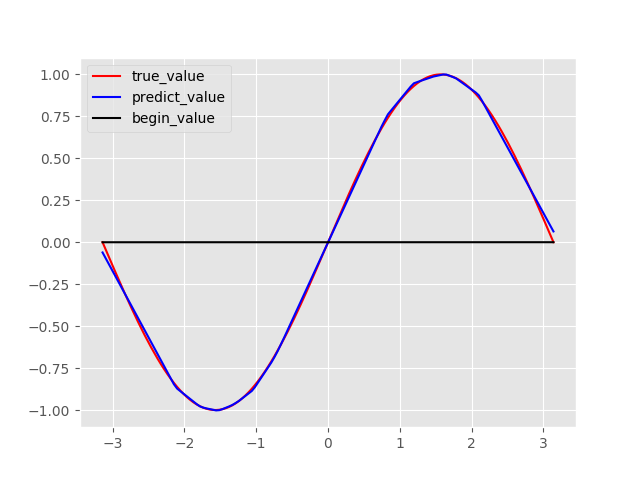
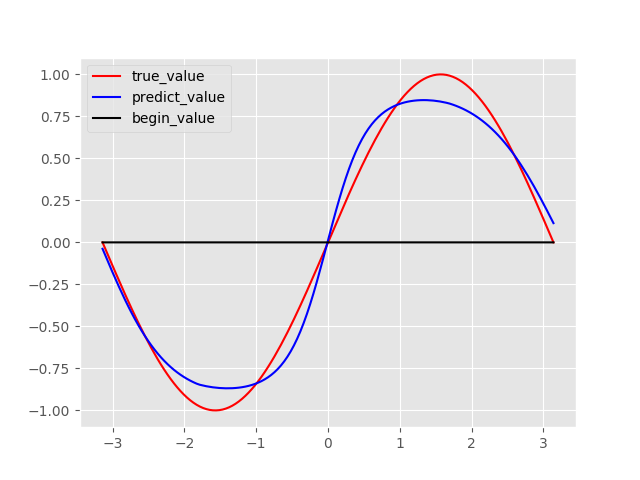
plt.plot(x,y,c='r',label='true_value')
plt.plot(x,y_pre,c='b',label='predict_value')
plt.plot(x,y_start,c='black',label='begin_value')
plt.legend()
plt.savefig('1.png')
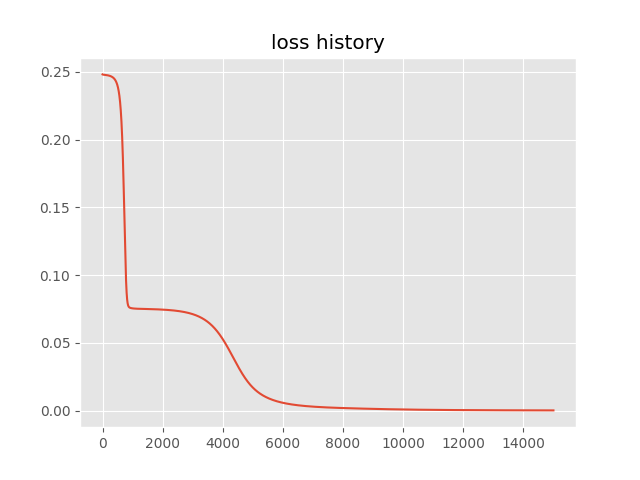
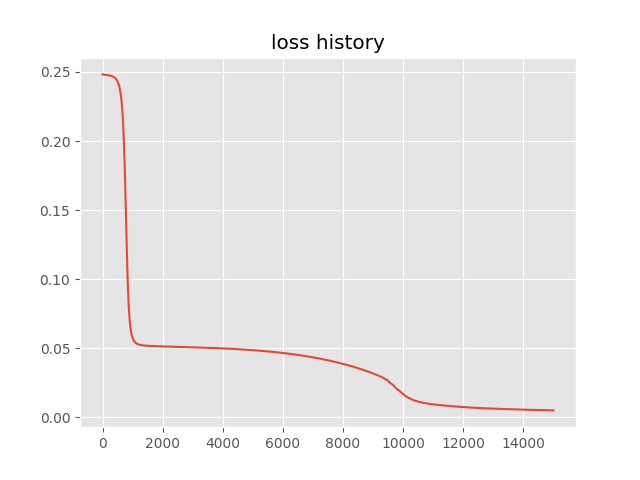
plt.figure()
plt.plot(np.arange(0,len(l)), l )
plt.title('loss history') 
# save the loss history.
plt.savefig('loss_t.png')