Learning From Data——Activation Function
上次lfd的博客讲了神经网络的一些基本内容,包括它的起源,前向传播以及后向传播。实际上,对于一个很重要的部分:activation function,只是简单提到。所以这次着重说一下不同的激活函数之间的区别。
你应该还记得有这么一段话:
上面的函数中,g为logistic函数,又叫sigmoid函数。当然这个函数不仅仅局限于sigmoid函数,也有relu函数,tanh函数:
$$
\begin{matrix}
g(z) = \frac 1 {1+e^{-z} } &(sigmoid)\
g(z) = \max(z,0) &(ReLU)\
g(z) = \frac{e^z - e^{-z} }{e^z + e^{-z} }& (tanh)
\end{matrix}
$$
实际上,实际上使用的也多是这三个函数,或者它们其中某个的变种。
同样,之前博客也说明了,为什么我们一定要在神经网络中使用非线性函数。所以在这里就不多提了。这篇博客,主要就介绍这3个函数的区别以及他们的使用场景。
sigmoid
Logistic Regression是一个非常基本的算法。在二元分类时候,它用的非常多。不过很遗憾的是,在neural network中,我们除了输出层几乎不使用这个函数。
Logistic Function(Sigmoid Function)的图像如下:
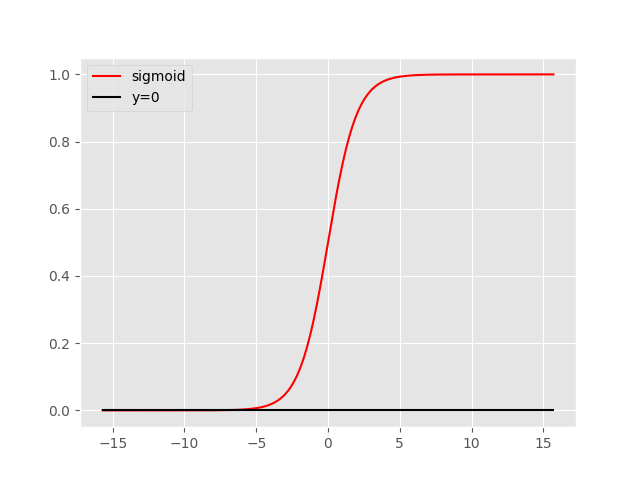
它的缺点很明显:
- 不是以0为中心的
- 当|x|比较大的时候,这个函数的梯度非常小,称为饱和区梯度扼杀。
- 指数运算较为复杂
因为1的存在,使得下一层的输入都是正的,那么下一层的梯度就会受限。此外,饱和区梯度太小,再加上指数运算比较复杂,这些使得sigmoid的梯度下降非常缓慢。
但是sigmoid函数也有非常大的优势,它一般作为输出层的激活函数,因为它将函数输出控制在0,1之间。实际运用中,除了输出层,几乎不用sigmoid函数。
tanh
tanh为双曲正切函数。它的图像如下:
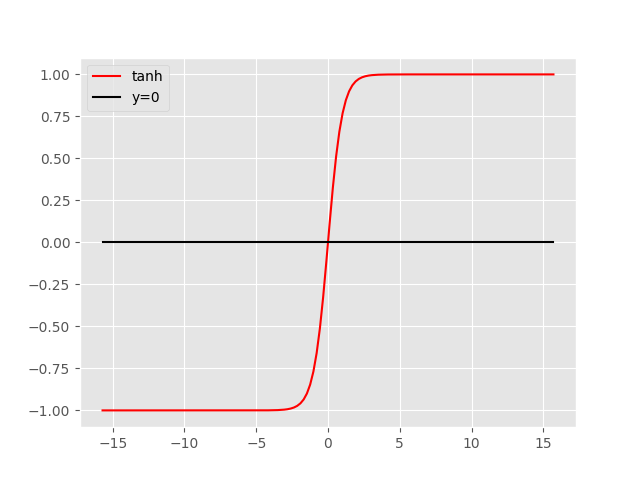
可以看到它和sigmoid函数非常相似,不过它的优点是以0为中心。不过呢它的缺点也比较明显,除了以0为中心,sigmoid有的缺点它都有。不过也因为这点,一般来说它表现的总是会比sigmoid函数更好。所以除了输出层,想要使用sigmoid的地方不如换成tanh函数。
ReLU
ReLU(Rectified Linear Unit)为线性整流函数,又称为修正线性单元。实际上它是目前最常用的激活函数。
它的正半轴没有饱和扼杀梯度的影响,而且运算也非常简单,使得它在神经网络中的收敛速度比其他的激活函数要快很多。它的图像如下:
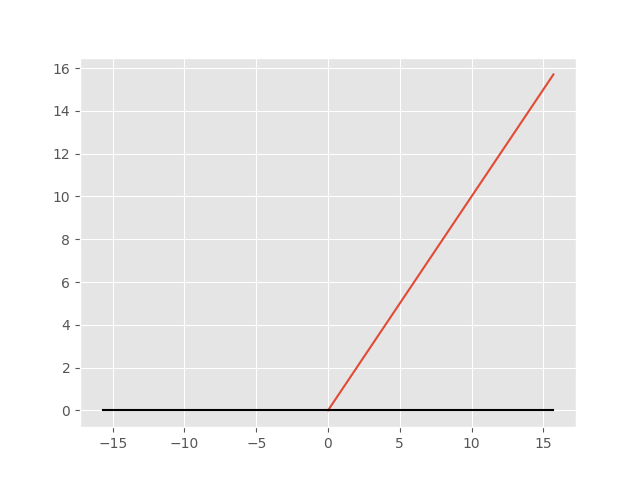
不过它也有缺点:输出不是以0为中心。而且当x小于0时候梯度将会被扼杀。
针对ReLU的不足有很多ReLU的改良版,如Leaky ReLU:g(x) = max(0.01z,z)等。这些在实际中比ReLU表现更好,但是使用ReLU依然是最多的选择,实际上ReLU是目前的神经网络的默认激活函数。
derivative of activation function
| function | derivative |
|---|---|
| sigmoid | $g’(x) = g(x)(1 - g(x))$ |
| tanh | $g’(x) = 1-g^2(x)$ |
| ReLU | $g’(x) =\left { \begin{matrix}0&x<0\1&x>0\end{matrix}\right .$ |