Learning From Data——Generative Learning Algorithm

Posted on 2018-10-29 Edited on 2023-10-21 In 数据学习课程

之前我们介绍的分类算法，包括，logistic regression，PLA甚至加上linear regression，他们都是试图找到一条线然后来将两种类别分开。这种算法叫做Discriminative Learning Algorithm，他们的由来，都是直接去估计$P(Y|X)$,这样的话根据新样本的X，从而预测Y。

接下来我们想介绍的是另外一种思路来解决分类问题。我们不再直接估计$P(Y|X)$,而是估计$P(X|Y)$.也就是，我们希望从当前的样本中学到X的特征看上去应该是什么样子，从鸡的样本中学到鸡的样子，从狗的样本中学到狗的样子。这样的算法叫做Generative Learning Algorithm（生成学习算法）。当然，我们最后要知道的还是$P(Y|X)$,不过根据Bayes理论可以知道：
$$
P(Y|X) = \frac{P(X|Y)P(Y)}{P(X)}
$$

我们知道：

$argmax_yp(y|x) = argmax_y \frac{p(x|y)p(y)}{p(x)} = argmax_y p(x|y)p(y) = WhatWePredict$

所以我们真正需要解决的是$P(x|y)P(y)$.

当然，如果想要求得P(X),可以通过全概率公式：$P(X) = P(y=1)\cdot P(X|y=1) +P(y=0)\cdot P(X|y=0)$.

下面介绍两个最常见的生成学习算法：Gaussian Discriminant Analysis(高斯判别分析)与Naive Beyas(朴素贝叶斯模型)。

Gaussian Discriminate Analysis

高斯判别模型主要用于输入是连续的时候，也就是X的特征值是属于实数集的。首先来复习一下多维高斯分布模型，它是高斯判别模型的基础：

一般来说，多维高斯分布简写为：X \tilde{} N(\mu,\Sigma).

$\mu \in \mathbb{R}^n$ 是平均向量。
$\Sigma \in \mathbb{R}^{n \times n}$是协方差矩阵。$\Sigma$是对称的SPD（ symmetric and positive definite matrix）.

它的概率密度函数如下：
$$
p(x;\mu,\Sigma) = \frac{1}{(2\pi)^{\frac n 2}\vert \Sigma\vert ^{\frac 1 2} } e^{-\frac 1 2(x-u)^T\Sigma^{-1}(x-u)}
$$

均值和协方差对分布有什么影响？利用一个二维的向量来说的话，有下面几张图可以看看：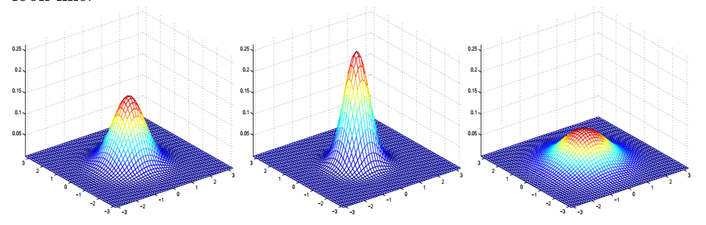

这三张图分别对应着协方差矩阵为$I，2I,\frac 1 2 I$的情况。其中
$I = \begin{bmatrix}
1&0\
0&1
\end{bmatrix}$.

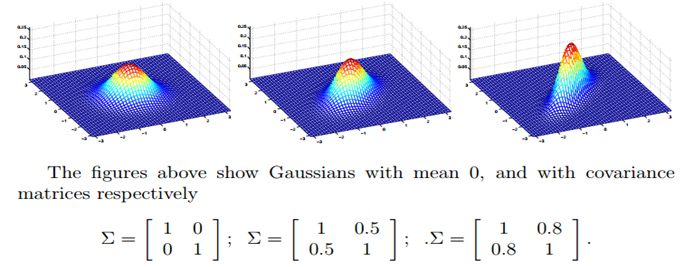
从上图又可以看出来，协方差矩阵非对角线的数字变化的时候，对它的图形似乎扭向一边了。实际上这代表了两个特征间的相关程度。

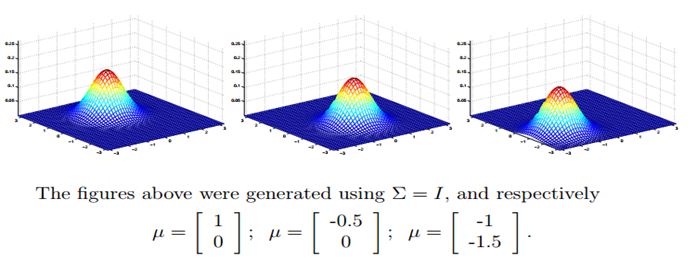
最后一个就是$mu$的变化，很显而易见，图形的中心改变了。

现在假如有一个分类问题，其中$X \in \mathbb{R}^n$,利用高斯判别模型的话，我们会有以下假设：
$$
y\tilde{} Bernuolli(\Phi)\
p(x|y=0)\tilde{}N(\mu_0,\Sigma)\
p(x|y=1)\tilde{}N(\mu_1,\Sigma)
$$
从上面看出来，我们对于两个模型的生成采用的$\mu$不一样，但是$\Sigma$一样，这样不光保证了两个模型的形状一样，简化了计算过程，最后可以用它们接触点的切线来当做分割线，从而实现与之前Discriminative学习算法的比较。

Note:现在n为向量的维度，而m为样本个数。

和往常一样，我们求它的log极大似然估计：
$$
\begin{align}
l(\Phi,\mu_0,\mu_1,\Sigma)&= \log \prod_{i=1}^{m}p(X_i,y_i;\Phi,\mu_0,\mu_1,\Sigma)\
&= \log \prod_{i=1}^m p(X_i|y_i;\mu_0,\mu_1,\Sigma)p(y_i;\Phi)
\end{align}
$$

上述的式子中的参数取值如下：
$$
\Phi = \frac 1 m \sum_{i=1}^m \mathbf{1}{ y_i = 1}\
\mu_b = \frac{\sum_{i=1}^m \mathbf{1}{y_i=b}X_i}{\sum_{i=1}^m \mathbf{1}{y_i=b} },b=0,1\
\Sigma = \frac 1 m \sum_{i=1}^m(X_i - \mu_{y_i})(X_i - \mu_{y_i})^T
$$

我们希望生成的模型如下：

如果画等高线图：

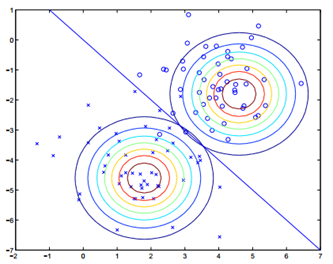
我们会发现找到一条线，它属于0或者1的概率是相等的。因此我们就找到了这条线。

GDA与Logistic Regression

在上面的推导过程中我们发现：
$$
\begin{align}
P(y=1|X;\Phi,\mu_0,\mu_1,\Sigma) &= \frac{p(X|y=1)p(y=1)}{p(X|y=1)p(y=1)+p(X|y=0)p(y=0)}\
&=\frac {1}{1+e^{-\theta ^TX} }
\end{align}
$$
上式中：$\theta = \begin{bmatrix} \log \frac{1-\Phi}{\Phi} - \frac 1 2(\mu_0^T\Sigma^{-1}\mu_0 - \mu_1^T \Sigma^{-1}\mu_1) \ \Sigma ^{-1}(\mu_0 - \mu_1)\end{bmatrix}$.

如果还记得上次讲过的exponential family，我们应该知道对于伯奴利分布$(y|x \tilde{} B(\psi))$的canonical link funtion是 $\log \frac{\psi}{1-\psi}$.

因此$\theta ^X = \log \frac{\psi}{1-psi} = \log \frac{p(y=1|X)}{p(y=0|X)} = \log \frac {p(X|y=1)p(y=1)}{p(X|y=0)p(y=0)}$

这意味着：如果$p(x|y)\tilde{}N(\mu,\Sigma)$,则$p(y|x)$是logistic function.但是从logistic regression是无法推出来GDA的。

如果我们的假设正确，GDA模型更高效，效果也更好，但是logistic regression因为比较简单，对于即使假设错误了依然有很好的鲁棒性。GDA最大化联合分布，而LR最大化的是概率分布。

所以我们发现，GDA并不像普通的学习算法那样需要去进行cost funtion的优化。这得益于我们假设整个正样本的X服从一个高斯分布。而之前的学习方法，每个样本因为X不同各个样本之间服从分布的参数都会不一致，也就是每个样本在给定y的时候有一个自己的分布（如逻辑回归，每个样本都有不同的概率，而它预测的是伯奴利分布，也就是每个样本服从不同的伯奴利分布；又如线性回归，每个样本有不一样的$\mu$）。

Naive Beyas

下面介绍朴素贝叶斯模型。它用来处理输入为离散数据时候的情况。假如有这么一个例子：垃圾邮件分类。如何定义邮件的特征？当然定义的是其中的单词了。但是这个世界上单词有很多很多，而垃圾邮件很可能更包含了很多无意义的字符组合，这样特征就更多了。

假设给一个大小为n的字典（这个n可能很大，50000或者100000），而一个邮件的特征值会像下面的样子：
$$
\begin{bmatrix}
1\
0\
.\
.\
.\
1\
.\
.\
.
\end{bmatrix} \begin{matrix}
a\
aadjsa\
.\
.\
.\
b\
.\
.\
.
\end{matrix}
$$

1或者0代表了在这个邮件中是否出现了。

现在希望对$P(X|Y)$建模。对于一封垃圾邮件：
$$
p(x_1,x_2,…,x_n|y) = p(x_1|y)p(x_2|y,x_1),…,p(x_n|y,x_1,…,x_{n-1})
$$
使用了概率论中的链式法则。这个规则我也不了解，概率论还需要学习

这样的计算是非常复杂的。因此朴素贝叶斯模型中有一个假设：$x_i$在给定y之后是条件独立的。这意味着：$p(x_n|y,x_1,…,x_{n-1}) = p(x_n|y)$.

所以$p(x_1,x_2,…,x_n|y) = \prod _{i=1}^np(x_i|y)$.

多变量伯奴利事件模型

$p(x,y) = p(y)p(x|y) = p(y) \prod _{i=1}^n p(x_i|y)$.

这个模型假设了每封邮件是以$\Phi_y$随机生成的。如果给定y，每个单词是独立的包含在信息里的，而这个概率为$p(x_i=1|y) = \Phi_{i|y}$.

这个模型参数如下：

$\Phi_y = p(y=1)$
$\Phi_{i|y=0} = p(x=1|y=0)$
$\Phi_{i|y=1} = p(x=1|y=1)$

同样的，接下来要做的依然是求log极大似然估计：

$$
\begin{align}
L(\Phi_y \Phi_{i|y=1},\Phi_{i|y=0}) &=\log \prod_{i=1}^m p(X_i,y_i)\
&= \log \prod_{i=1}^m p(X_i|y_i)p(y_i)\
&= \log \prod_{i=1}^m \prod_{j=1}^np(x_j|y_i)
\end{align}
$$

不难想象，各个参数的取值如下：
$$
\Phi_y = p(y=1) = \frac 1 m \sum_{i=1}^m \mathbf{1}{y_i=1}\

\Phi_{j|y=b} = \frac {\sum_{i=1}^m \mathbf{1}{y_i = b} \cdot \mathbf{1}{ x_j=1} }{\sum_{i=1}^m \mathbf{1}{y_i = b} },b=0,1
$$

当给了一个新的样本的时候，我们计算$p(y=1|x)$:

$$
\begin{align}
p(y=1|X) &= \frac{p(X|y=1)p(y=1)}{p(X)}\
&= \frac{p(y=1)\prod _{i=1}^n p(x_i|y=1)}{p(X|y=1)+p(X|y=0)}\
&=\frac{p(y=1)\prod _{i=1}^n p(x_i|y=1)}{p(y=0)\prod _{i=1}^n p(x_i|y=0)+ p(y=1)\prod _{i=1}^n p(x_i|y=1)}
\end{align}
$$

然后根据概率是否大于0.5来进行预测。

Laplace Smoothing

这个模型是有一个缺点的：如果新的样本的单词从来没有在训练集合里出现过，那么：

$$
\Phi_{j|y=b} = \frac {\sum_{i=1}^m \mathbf{1}{y_i = b} \cdot \mathbf{1}{ x_{i,j}=1} }{\sum_{i=1}^m \mathbf{1}{y_i = b} } = 0,b=0,1
$$

也就是垃圾邮件和非垃圾邮件里出现它的概率都为0.那么最后预测结果为$\frac 0 0$,这就没法计算了。

所以我们需要进行Laplace平滑。对于没有出现过的词，我们给他赋一个较小值，而不是让他为0：
$$
\Phi_j = \frac{\sum_{i=1}^m \mathbf{1}{z_i = j}+1}{m+k}
$$

为了最后使得$\Phi_j$的和为0,所以k为类比的个数，即$\sum_{i=1}^k\Phi_i = 1$。

所以最后的估计就成了下面的样子：
$$
\Phi_{j|y=b} = \frac {\sum_{i=1}^m \mathbf{1}{y_i = b} \cdot \mathbf{1}{ x_{i,j} = 1} +1}{\sum_{i=1}^m \mathbf{1}{y_i = b} +2},b=0,1
$$

除此之外其他地方是一样的。

Naive Bayes and Multinomial Event Model

现在有一个新的方法，就是多项式模型。

现在$x_i \in {1,…,\vert V \vert}$,其中|V|为字典的长度。而n为信息的长度，也就是现在每个样本的特征数已经不一样了，因为我们没法保证每封信长度一样。

对字典中每个词都进行编号：

dictionary id	1	2	…	1300	…	2400	…
word	a	aa	…	free	…	gift	…

多项式模型中有下面几个假设：

信息随机地被以概率$p(y)$生成
$x_1,x_2,…,x_n$独立同分布
$p(x_1,x_2,…,x_n,y) = p(y)\prod _{i=1}^n p(x_i|y)$

假设$p(x_i=k|y)$对所有的$k$来说都相等。
则该模型参数如下：

$\Phi_y = p(y)$
$\Phi_{k|y=1} = p(x_j = k|y=1)$ for any $j \in {1,…,n}$
$\Phi_{k|y=1} = p(x_j = k|y=0)$ for any $j \in {1,…,n}$

则出现训练样本的概率为:
$$
\begin{align}
L(\Phi_y,\Phi_{k|y=0},\Phi_{k|y=1}) &= \prod_{i=1}^m p(x_i,y_i)\
&= \prod_{i=1}^m p(y_i)p(x_i|y_i)\
&=\prod_{i=1}^m p(y_i) \prod_{j=1}^{n_i} p(x_{i,j}|y_i;\Phi_y,\Phi_{k|y=1},\Phi_{k|y=0})
\end{align}
$$

各个参数取值如下：
$$
\Phi_y = \frac 1 m \sum_{i=1}^m \mathbf{1}{y_i=1}\
\Phi_{k|y=1} = \frac{\sum_{i=1}^m \mathbf{1}{y_i=1}\cdot (\sum_{j=1}^{n_i}\mathbf{1}{x_i=k}) +1}{\sum_{i=1}^m \mathbf{1}{y_i=1}+|V|}\
\Phi_{k|y=0} = \frac{\sum_{i=1}^m \mathbf{1}{y_i=0}\cdot (\sum_{j=1}^{n_i}\mathbf{1}{x_i=k}) +1}{\sum_{i=1}^m \mathbf{1}{y_i=0}+|V|}
$$

最后，预测值为：$p(y=1|x) = \frac{p(x|y=1)p(y)} {p(x|y=1)+p(x|y=0)}$