数学——Newton Method

Posted on Edited on In

梯度下降时候，有时候我们可以使用Newton Direction.牛顿迭代法其实大家听起来很熟悉的。

首先来说明下，简单的牛顿迭代法的原理。牛顿迭代法是求近似解的一个办法，很多时候解无法算出来，我们只能用牛顿迭代法来一步步逼近。

首先给个很直观的例子，也就是一维的函数。先观看一下下面的gif。

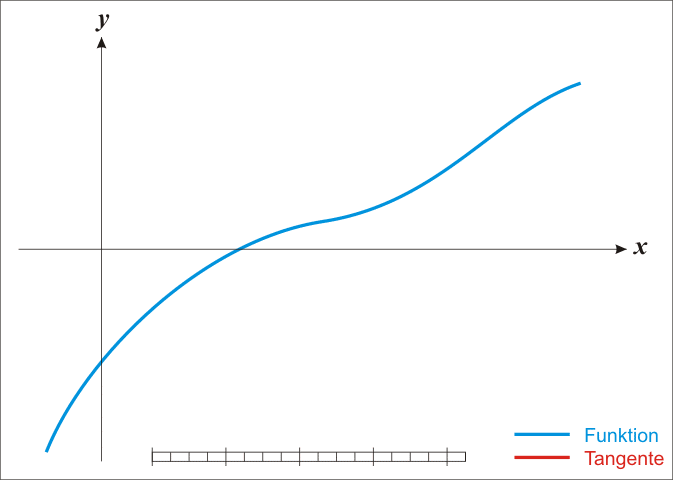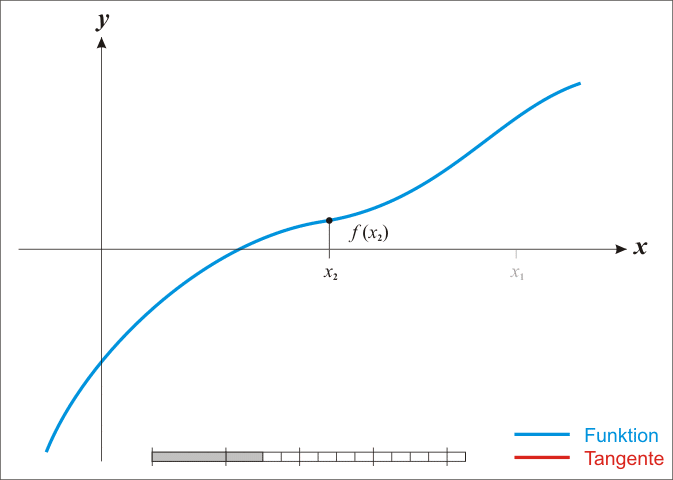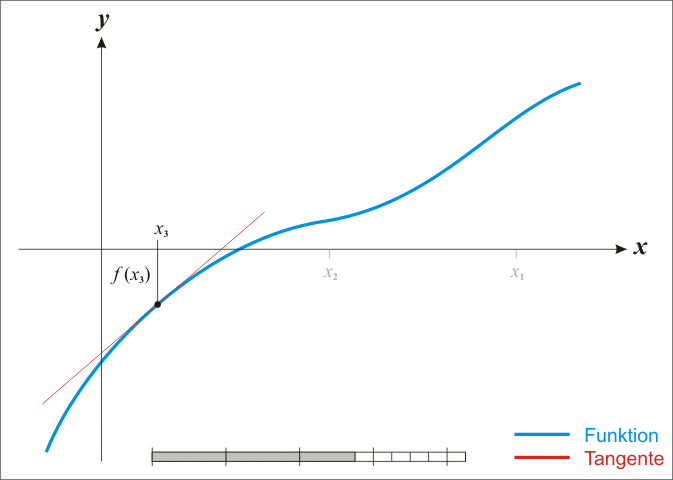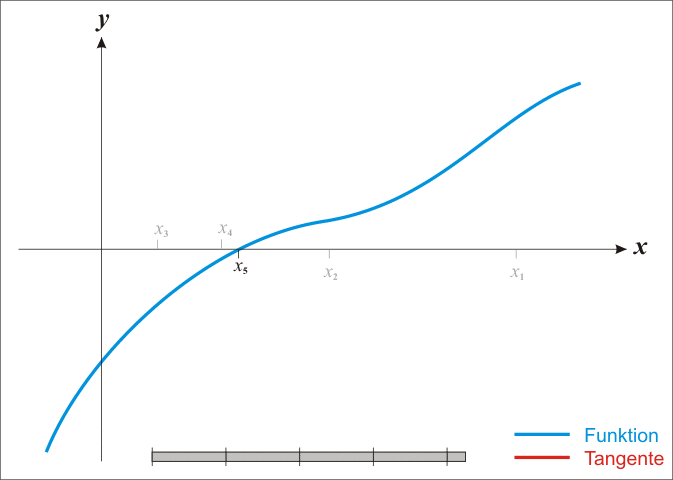
为了求得f(x)=0f(x) = 0,我们从图上直观看到可以一直这样逼近，最终会逼近到f(x) = 0的解。

原理是，如果我们将f(x)一阶泰勒展开,得到： f(x)≈f(x0)+f′(x0)(x−x0)=g(x) f(x) \approx f(x_0)+f'(x_0)(x - x_0) = g(x)

而上式g(x) = 0是很容易解决的：x=x0−f(x0)f′(x0)x = x_0 - \frac {f(x_0)}{f'(x_0)}.

因为泰勒只是近似，因此上述得到的解并不是真正的解，只是离原有的解更接近了。也就是，牛顿迭代法种，下一步更新策略为:$x_ {n+1} =x_n - $.

如何将牛顿迭代法用来解决优化问题？我们知道优化问题，想要得到最小值，或者最大值，在该点导数是为0的，这个问题就变成了，如何找到导数为0的点，那么就很简单了，对于一维函数的优化问题迭代步骤如下:$x_ {n+1} =x_n - $.

多维函数来说，情况较为复杂一点，因为高纬度的二阶导数实在是很多。不过原理也是变化不大的，我们需要利用Hessian矩阵：

xn+1=xn+1−Hf−1(xn)∇f(xn)x_ {n+1} = x_ {n+1}-H_f^{-1}(x_n)\nabla f(x_n).

Hessian矩阵定义如下： Hf=[∂2f∂x12∂2f∂x1∂x2...∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x2∂x2...∂2f∂x2∂xn...∂2f∂xn∂x1∂2f∂xn∂x2...∂2f∂xn2] H_f = \begin{bmatrix} \frac {\partial^2f}{\partial x_1^2}& \frac {\partial^2f}{\partial x_1 \partial x_2}&...&\frac {\partial^2f}{\partial x_1 \partial x_n} \\ \frac {\partial^2f}{\partial x_2 \partial x_1}& \frac {\partial^2f}{\partial x_2 \partial x_2}&...&\frac {\partial^2f}{\partial x_2 \partial x_n} \\ ...\\ \frac {\partial^2f}{\partial x_n \partial x_1}& \frac {\partial^2f}{\partial x_n \partial x_2}&...&\frac {\partial^2f}{\partial x_n^2} \end{bmatrix}

可以看到的是，如果维度较高，这个海森矩阵的求逆是非常耗费时间的。一般来说，优化问题时候，维度较低的情况下，它的效果还是非常好的，比梯度下降更快。