机器学习——Regularization
上篇博客说了overfitting的情况,有一些比较高级的处理overfitting的办法,其中有一个就是regularization,中文中叫做正则化。
从前面的nonlinear transform中也说明了,复杂的假说一般会包括了简单的假说。例如一个2次的假说,与10次的假说,他们的区别,就是10次的比二次的多了更多三次及以上的特征。也就是二次假说实际上是十次假说加上了一个限制:三次及以上的特征前面的权重(w)为0.这样就使得假说变得简单了不少.
如果放宽这个限制,假如较为简单的模型特征量有r个,在复杂模型中,最多有r个特征的权重不为0,在一定程度上,也可以很好的减少这个复杂度。只不过让人遗憾的是,在这样的假说中选出最佳的$\mathbf w$(权重向量)被证明了是一个NP-hard问题,没有一个很好的解决办法.
如果个数是整数,要挑出最好的,很容易有NP-hard问题,但是将这个拓宽到实数领域,我们往往可以通过数学工具得到最佳解。例如在这里,我们继续拓宽这个限制:让这些$w^2$和小于一个常数$C$,似乎也可以起到类似的效果。
为了简化问题,举个很简单的例子如:对于只有一个特征量的样本集,$H_2 = w_0+w_1x+w_2X^2$,而$H_ {10} = w_0+w_1x+w_2x^2+…+w_ {10}x^{10}$.
对于$H_2$来说,$H_ {10}$中限制为$w_3 = w_4 = w_5 = …= w_ {10} = 0$.
对于上面说的第二种假设,$H_ {10}$限制为:$\sum _ {n = 0} ^{10} [[w_n \ne 0]] \leq 3$.
对于第三种假设,$H_ {10}$限制为:$\sum_ {n = 0}^{10} w_n^2 \leq C$ 即$W^TW \leq C$.
那么,我们已经知道了最后一个才有可能求得最佳解。如何去做?
高维度的figure我们无法想象,我也不知道怎么去称呼,但是如果是二维,这个限制是一个圆,如果是三维,这个限制是一个球。假设我们依然称这个限制为一个球,而没有限制的最低点不在这个球内。因此梯度下降的结果就是达到了球的边缘,但是依然想要走下坡路。无路可走的情况,是梯度与该法向量的方向平行了,而只要梯度与该法向量的方向不不平行,我们总是可以朝着某个方向走使得$E_ {in}$继续减少。因此这个过程终止的时候,就是该点的法向量与$E_ {in}$的梯度平行了,而值得注意的是边缘某点的法向量实际上就是$W$.如果我们称做这个结果$W$为$W_ {REG}$,那么有个结果:$W_ {REG} = \lambda ▽E_ {in}$.
其中这个$lambda$是一个常熟.我们知道,线性回归中梯度为$▽E_ {in} = \frac 2 N (X^TX - Y^TXW)$,为了简化,我们将$\lambda$写为$ \frac {2\lambda} N$,最后得到:
$$
▽E_ {in}+ \frac 2 N \lambda W_ {REG} = 0.
$$
如果$\lambda$提前知道,那么我们就可以求得$W_ {REG}$的值.
如果对上式左边求积分可以得到:
$$
f(W) = E_ {in} + \frac \lambda N W_ {REG}
$$
所以可以很神奇地发现,对于原来的问题的求解可以很有效地转变成了求$f(W)$的最小值,它就是正则化后的$E_ {in}$,因此新的$cost-function$变成了下面的样子:
$$
min_ {W \in R^{Q+1} } \frac 1 N \sum _ {n = 0} ^N (\mathbf{w}^T \theta(X_n) - y_n)^2 + \frac {\lambda} N \sum {q=0} ^Q w_q^2
$$
tips:对于多项式正则化,因为一般来说我们会将特征值的范围限定到$[-1,1]$(原因以后再探讨),这导致高次项的影响可能变得非常小,为了处理这种情况需要用到一个正交化处理,关键词“Legendre polynomial”。效果更好。需要了解更多的话可以去搜索.
$\lambda$由$C$确定(这是不严谨的说话。但是实际中给定\lambda就可与将$W$限定到一个范围,因此给出C的人也更容易给出一个$\lambda$),实际应用时,给$\lambda$一个很小的值就可与很好地处理过拟合的情形,如果过大,可能会出现欠拟合的情况.
接下来需要继续说明的是regularization,与vc理论之间的关系。实际上,即使加上了regularization,对于一个假说来说,在数学计算上它的vc dimention依然很大,依然会付出很大的代价。但是regularization的作用是什么?它将我们需要寻找的范围局限在了一定范围内,在这个范围内,可能都是比较好的$h$,因此有效的vc dimension减少了,也就更有可能得到比较好的$E_ {out}$。
如何选择regularizer?
1.首先,如果我们知道目标函数的一些特点,就可以指引我们选择一些好的regularizer,比如:如果知道目标函数是偶函数,可以只对奇次项的特征进行正则化。
2.选择平滑的,如$\sum _ {q=0} ^ Q |w_q|$.这个也叫L1 regularizer(L1正则化).相对于L2来说它效果往往更好一点,因为更加平滑,但是不好解。
3.选择好优化的,如L2,也就是上文提到的。
除此之外,还有$\lambda$的选择。如图,不同的noise级别需要的$lambda$也不同:
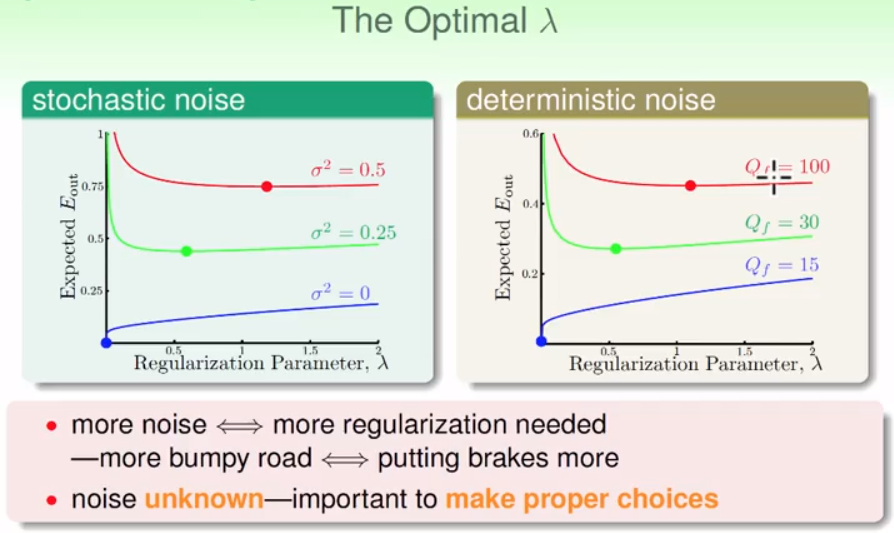
如何选择一个合适的$\lambda$也非常重要,这就需要用到下一节所讲的Validation。