机器学习——Nonlinear Transformation
之前我们学习的所有模型,都是linear model。我们做的都是用一条直线(或者平面等)来分类,或者拟合,或者是通过该直线来预测概率。但是现实中很多时候线性不一定能做得很好。如下图: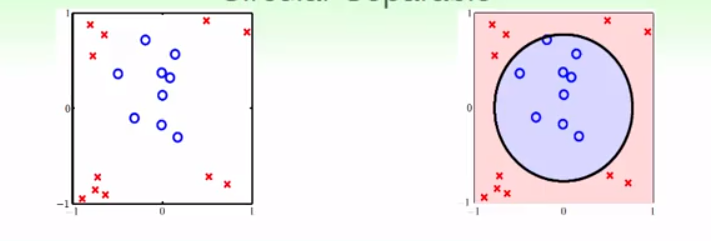
似乎用一个圆,能更好地对这些样本进行分类。实际上,上图的分类的依据是:
$$
h(X) = sign(0.6-x_1^2-x_2^2)
$$
因此,这样我们就引入了二次假设(quadratic)。
在上式中,如果我们令$z_0 = x_0 = 1, z_1 = x_1^2 ,z_2 = x_2^2$,那么就发现,实际上上面中对于$x$的二次假设实际上转换为了对$Z$的线性假设。一个样本在x空间上是很难线性分割的,无论怎样都不能得到较好的$E_ {in}$,但是展开到z空间上也许就是线性可分的了。
因此怎么做实际上很简单,之前的训练集是$D$,我们通过展开到z空间来得到训练集$D’$,用训练集来进行之前的用于线性模型的训练。
通过这个,我们仿佛进入了新世界:我们可以任意来构建多项式(特征转换),达到非线性学习的结果。
但是世界上不会天上掉馅饼。我们知道不会有这么白白的好事发生。既然多项式这么强大,它必然会付出更多的代价,下面我们来简单说明下它的price。
假如原始特征有d个,我们构建的是最高次为Q的Q次多项式($Q \leq d$)。那么,构造的新的样本集会有多少个维度?
$$
\Phi _Q(X) = \left ( \begin{matrix}
1,\
x_1,x_2,…,x_d,\
x_1^2,x_1x_2,…,x_d^2,\
…,\
x_1^Q,x_1^{Q-1}x_2,…,x_d^Q\
\end{matrix} \right )
$$
假如我们乘转换后的维度是$\overline d$,则 $\overline d = C_ {Q+d}^d-1 =>O(Q^d)$(如何得到这个值需要排列组合知识,在此处知道即可).
这意味着$\overline W$是($1+\overline d$)维的向量,而转换后的$vc dimension \leq \overline d+1$(之前的VC bound中证明过了二元分类维度为d的时候,vc dimension为d+1).vc dimension可能会增加很多,也就意味着我们需要非常多的资料可能才能得到较好的准确度,同时也会极大地增加存储空间,以及算法的学习速度。
我们列出次数为1-Q时候的维度如下:
$$
\Phi _0(x) = (1)
$$
$$
\Phi _1(x) = (\Phi _0(x) , x_1,x_2,…,x_d)
$$
$$
\Phi _2(x) = (\Phi _1(x) , x_1^2,x_1x_2,…,x_d^2)
$$
…
$$
\Phi _Q(x) = (\Phi _ {Q-1}(x),x_1^Q,x_1^{Q-1}x_2,…,x_d^Q)
$$
因此:我们可以得到:
$H_0 \subset H_1 \subset H_2 \subset H_3 \subset … \subset H_Q$;
从而得到:
$ d_ {vc}(H_0) \leq d_ {vc}(H_1) \leq d_ {vc}(H_2) \leq … \leq d_ {vc}(H_Q)$;
而对于$E_in$来说,不错的消息是$E_ {in}$是在不会变大的。因为它最多最好的线与之前一样:
$ E_ {in} (g_0) \geq E_ {in} (g_1) \geq E_ {in} (g_2) \geq … \geq E_ {in}(g_Q)$;
更重要的一件事,不知道你是否还记得这个学习曲线:
从上面可以看出来,维度个数增加,$E_ {out}$并不是一直下降的,最好的维度个数是在中间某个地方。而$E_ {in}$从来就不是我们关注的重点,我们尽可能减少他,是为了得到更好的$E_ {out}$,而过分增加维度个数,可能会本末倒置。$E_ {out}$才是我们想要的。
实际中,我们在学习时候应该先从低的维度开始,再慢慢向上增加,直到得到想要的$E_ {in}$,往往线性的学习并不像人们想象中的那样效果很差,可能从较低的维度就可以得到较好的结果。如果一开始就用很多的维度,可能直接得到了很好的$E_ {in}$,但是泛化能力却很差。
最后,要注意,有的人说,刚开始举得例子中,如果通过可视化,我们直接用 $s(X) = w_0 + W_1 x_1^2 + W_2x_2 ^2$,这样看起来,似乎维度只有3个,实际上类似的还有$s(x) = w_0 + W_1( x_1^2 + x_2 ^2)$,似乎维度只有两个,甚至是可以降到0个。但是这实际上是人脑学习的过程,我们已经替机器学习了不少,因此最后的泛化结果可能并不是我们想象的那么好,因为真实的代价还是存在的。而且,高纬度的可视化是很难做到的。
因此,使用多项式并不见得就是好的,我们要结合实际情况来进行学习。