机器学习——Multiclass(OVA and OVO)
目前,我们对二元分类已经有了不少的了解,可以用多个线性模型去实现二元分类。但是生活中遇到的往往不是是非题,而是选择题,尤其是图像识别问题中,我们往往需要识别多个物体。如何通过之前实现的二元分类,来实现多元分类呢?
这里介绍两种思路,一个是OVA(One Vesus All),另一个是OVO(One Vesus One)。
OVA(via Logistic Regression)
要想进行多元分类,我们首先想到的是对每一种类型进行是非判断。理想中,这样似乎不错,找个物体,哪一种类型的判断说是,就是该类型,但是现实往往不尽人意。
假如有下图所示的一个样本集:

可以看到一共有四类,分别对每个类型进行是非判断,可以得到下面的4条线来分类:
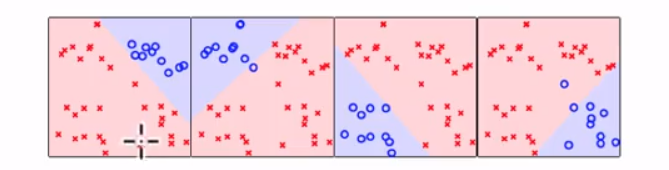
从左至右分别是正方体,菱形,三角形,五角星得到的线。
融合到原来的图形上:

对于上图中,有几个部分区域的样本可以很明确的判断出来是什么类型,但是其他部分区域,要么是多个类型都说是,要么没有一个类型说是,这就让我们无法进行判断。
我们很容易想到既然用明确的是非无法进行判断,如果使用概率会不会好一点。因此要使用logistic regression。
使用logistic regression进行的还是上面的步骤,得到的是是各个类型的概率。选择概率最高的,就可进行分类。

下面的分类图是利用上述方法进行分类得到的结果,可以看到对每个区域,都能为它制定一个类别。值得注意的是logistic function是单调增函数,因此比较概率的时候我们并不用真的求出来大小,而只用比较$s(X)$的大小即可。
具体步骤如下:
(1) for $k \in Y$, obtain W_ {[k]} by running logistic regression on $D_ {[k]} = \left { (X_n,y’n = 2[y_n = k] - 1) \right} {n=1}^N$.
(2) return $g(X) = argmax_ {k \in y}(W_ {[k]}^TX) $
***注:argmax是一种函数,函数y=f(x),x0= argmax(f(x)) 的意思就是参数x0满足f(x0)为f(x)的最大值;换句话说就是 argmax(f(x))是使得 f(x)取得最大值所对应的变量x。arg即argument,此处意为“自变量”。在上式中为结果为某个k$(k \in y)$。
上面的方法很简单的就可以实现了多元分类。但是上面的算法有个缺点,一对多,当种类k特别多时候,很容易造成不平衡的情况,一个不好的算法但是却得到了很好的$E_ {in}$,影响最后的分类结果。因此希望可以找到一种方法来解决这个问题。
OVO(via Binary Classification)
OVO是一对一的算法,可以很好的解决上面最后留下来的问题。它的思想是这样的,从k个类别中挑出两种类别来进行学习,每次学习都可以得到一个用来区分的$W$,一共可以得到$C_k^2$种。
这里得到的$W_i$与上面的办法用途是不一样的,它直接用来做二元分类(+1 or -1),而不是得到一个概率。通过两两组合进行二元分类的学习,我们得到了$C_k^2$个分类器,每个分类器都会对放入的样本进行一个明确的分类。下图是上面的样本集得到的几个分类器: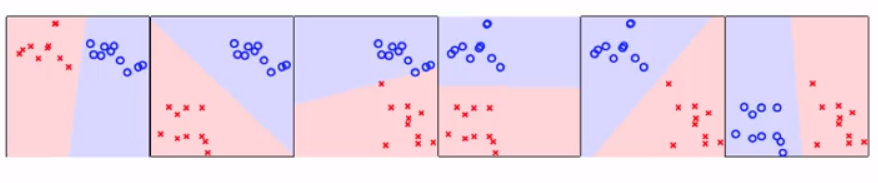
从左到右,分别是对[菱形,方块],[三角形,方块],[五角星,方块],[菱形,三角形],[菱形,五角星],[三角形,五角星]进行二元分类。
进行预测时候,取一个样本,经过6个分类器来预测,6个分类器得到不同的结果,但是每个都会对该样本的类别进行明确的预测,类似于投票,最后我们选择得票最多的类别。
下图为用OVO分类得到的结果:
OVO算法的主要过程如下:
(1) for ($k,\zeta$) $\in Y \times Y$, obtain $W_ {[k,\zeta]}$ by running linear binary classification on $D_ {[k,\zeta]} = \left { (X_n,y’_n = 2[y_n = k] - 1):y_n = k or y_n = \zeta \right }$
(2) return $g(X) =$ $tournament$ $champion$ $\left {W^T_ {[k,\zeta]}\right }$
总结
上面就是两种用在多元分类上的算法,他们都是很简单并且非常常见的算法。两个算法运行速度都很快(OVO虽然增加了分类器的个数,但是用来学习的样本量会减少很多)。OVO的缺点是如果类别真的非常大,那么分类器个数可能过多,会占用较大的空间,一定程度上也会影响速度,但是它有较高的稳定性,减少出现不平衡的情况。