机器学习——linear model for classification

到目前为止，已经学习了3个线性模型了，他们都使用到了$score = W^TX$(后文中简写为$s$)，使用特征间线性组合来打分，通过分数来做后续的处理。

linear regression用于分类前面有一篇博客已经说明，现在我们想要知道，logistic regression 是否也可以用于分类？毕竟线性回归的错误对于二元分类来说是一个很大的上界，这意味着它的效果虽然不差，但可能错失更好的。而PLA找到一个最小的$E_{in}$是NP-hard问题，只能使用改进的POCKET算法。我们希望看到logistic regression用于二元分类可以有更好的表现。

与之前的步骤一样，逻辑回归中，$E_{in} = \sum_{n = 1}^{N} \ln{1 + e^{-y_nW^TX_n} }$，我们对比的是单个样本的错误，就写作$err_{name}$好了。

为了让这3种模型都有较为清晰的对比，我们对PLA以及线性回归的错误衡量也做处理，如下：

method	linear classification	linear regression	logistic regression
err	$[sign(ys \neq 1)]$	$(sy-1)^2$	$\ln{1+e^{-ys} }$

将它们的曲线绘制到一张图上，可以得到下面的结果：

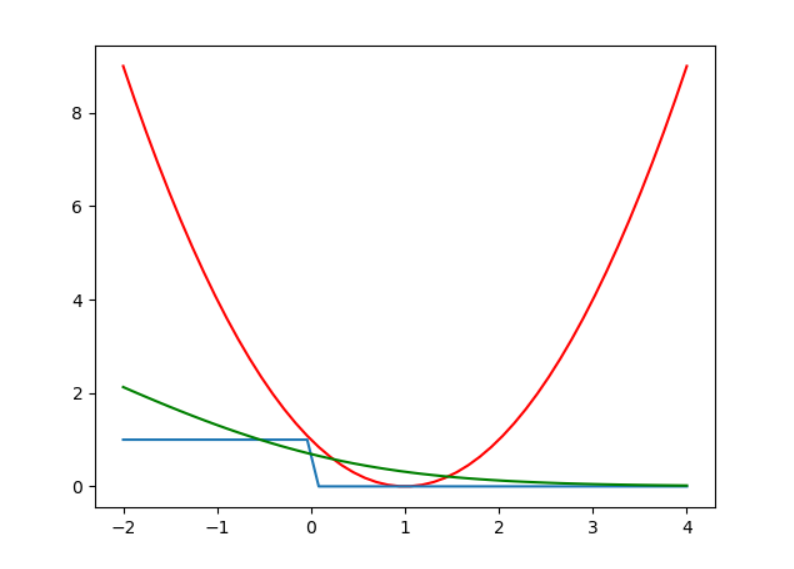
其中蓝色是linear classification的错误，红色是linear regression的错误，绿色是logistic regression。坏了，绿色的线并不总是大于蓝色的线，这意味着我们无法像之前一样，简单地将$E_{in}(linear classification)$换成$E_{in}(logistic regression)$。

实际上，之前我们选择用$ln$函数是因为这是最常见的，只是将乘法换成加法，理论上我们可以取任何对数，如，将对数函数换为$log_2^x$,就可以得到另外一副曲线图：

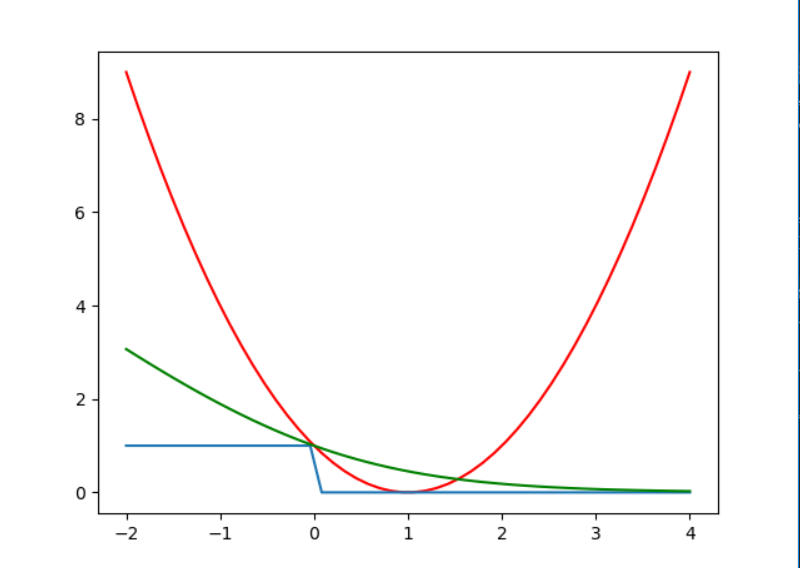
这样就可以满足我们的需要，也方便下面的证明。
我们称使用$ln(x)$函数的错误为$err_{ce}$，使用$log_2(x)$的为$err_{sce}$，则由上图可以知道：

$err_{0/1}(s,y) \leq err_{sce}(s,y) = \frac 1 {\ln2} err_{ce}(s,y)$，
（由换底公式：$\frac {\ln x}{\ln2} = log_2x ）
也就可以知道：
$$
E_{in}^{0/1} \leq E_{in}^{sce} = \frac 1 {\ln2} E_{in}^{ce}
$$

同样的道理：
$$
E_{out}^{0/1} \leq E_{out}^{sce} = \frac 1 {\ln2} E_{out}^{ce}
$$

因此，我们可以像之前一样推导：

$$
E_{out}^{0/1} \leq E_{in}^{0/1}+ \Omega ^{0/1} \leq \frac 1 {\ln2} E_{in}^{ce}+\Omega ^{0/1}
$$

同样，从另一个方向也可以推导：

$$
E_{out}^{0/1} \leq \frac 1 {\ln{2} } E_{out}^{ce} \leq \frac 1 {\ln2} E_{in}^{ce}+\Omega ^{ce}
$$

无论哪个，都可以证明，logistic regression是可以用于二元分类的。而上面的图像也说明了，他的效果比线性回归更好，bound更紧一点。

在实际应用中，我们使用linear regression来初始化$W$，然后通过POCKET或者logistic regression来进行后面的步骤，而且logistic regression更为常用。

注：上面推导中，判断都是以s=0为界定，对应到logistic regression也就是概率为0.5为界定。