机器学习——linear regression与linear classification

上一篇博客介绍了线性回归模型，但是不知道大家是否有这样的感觉：它与之前的PLA算法似乎有很多类似之处。

这两个算法都在使用线性的方法，也就是它们都是通过$y_n = W^TX_n$来计算出$y_n$，只不过PLA算法通过$y_n$来判断第n个样本的分类，而线性回归直接使用$y_n$来作为它的预测值。

线性回归中，$y$的值的范围是整个实数，从另一方面想，线性classification的$y$取值只有+1，-1两个取值，这两个值当然也是实数，我们是否能将线性回归算法用作于线性分类中呢？

要思考这个问题，首先要决定如何将线性回归用于线性分类：对样本集${X_n,Y_n}$利用线性回归来进行学习，得到$W$，然后通过$sign(y’_n)$（其中$y’_n = W^TX_n$）来对该样本进行分类。与PLA的区别是PLA一直在尝试各种不同的$W$，而线性回归直接得到一个自己认为最好的$W$。但是实际上它们的Hypothesis都是一样的。

这个算法是否可行，需要来检查它的泛化能力，也就是它的$E_{out}$是否像PLA算法一样有个上界。首先，我们观察两个算法对于错误的衡量有什么区别（注：以下错误都是单个样本的错误）：

category	$E_{in}$
linear classification(PLA)	$y \neq y’$
linear regression	$(y - y’)^2$
linear regression to classification	$y \neq sign(y’)$

在上面的表格中，我加了一行，也就是利用线性回归算法来进行线性分类时候的$E_{in}$，这意味着它们的$y’$是一样的(实际上$y’$代表的应该是最终的预测值，这里正确的写法应该是$h(X)$,此处只为了方便区分PLA)。

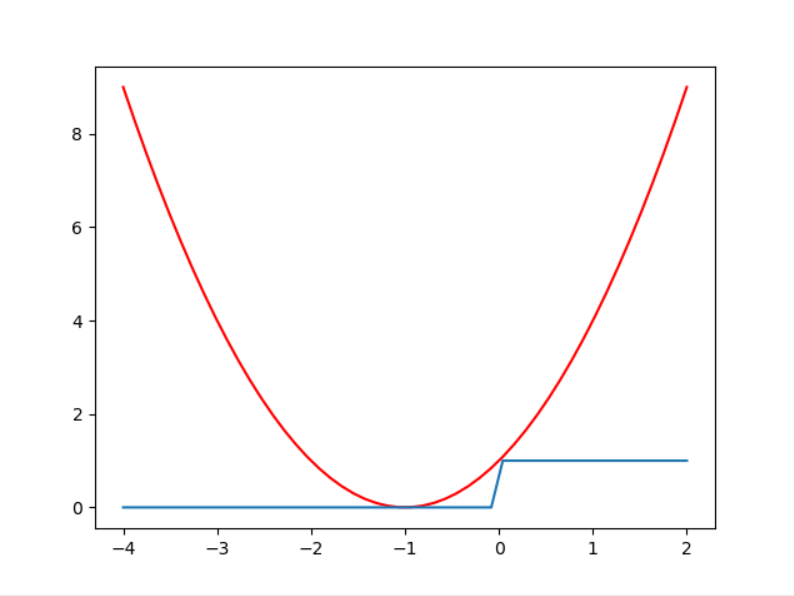
如果画出y = -1 与 y = +1 时候的曲线图，我们可以清晰地观察到，线性回归得到的错误永远是大于利用线性回归进行分类的错误的：

y = +1时：

y = -1时：

而通过之前vc bound那一节我们可以知道：

$$E_{out} \leq E_{in}(classification)+\sqrt {…}$$

也就可以得到：

$$E_{out} \leq E_{in}(regression) +\sqrt {…}$$

这意味着，只要linear regression的$E_{in}$做的足够好，那么使用线性回归来做线性分类，往往也能取到比较好的效果。

实际中，我们也可以使用线性回归与PLA算法结合，先通过线性回归得到W，然后因为给了PLA或者POCKET算法一个好的初始点，它能更快得到最后好的结果。