机器学习——VC bound
上次的Hoeffding不等式那篇,证明了一个hypothesis集合是有限集合,那么学习是可行的。
如果定义$E_ {in}$是资料上的错误率,$E_ {out}$是整体的错误率,我们证明的结果,如果N足够大,那么很大概率上,$E_ {in} \approx E_ {out}$.我们只需要在有限的集合利用里学习算法选出一个$E_ {in}$最低的,就可以实现学习,因为很大概率上它对整体分类后的错误率也是与$E_ {in}$差不太多的。
先思考一个问题,H的大小影响的了什么?学习需要做的有两个:1. 保证$E_ {in} \approx E_ {out}$ 2.找到一个h使得$E_ {in}很小$。
如果H集合过大,那么我们不容易保证第一个条件,但是如果集合过小,我们不一定能找到一个h使得它甚至在测试数据上有很好的表现。
上次博客留下来了一个问题:如果这个$H$集合是无限集合呢?例如之前实现的PLA算法。那我们怎么保证在无限的集合上,学习是可行的呢?
首先,我们来观察上次得到的hoeffding不等式:$P_ {baddata} \leq 2te^{-2\epsilon ^2N}.如果其中t->$\lnfty$,那么这个不等式实际上是没有意义的,因为右边的值将会远大于1,但是说一个概率小于等于1那是废话。
仔细想想,那是因为我们的union bound太宽松了。它们实际上会有很多重叠的部分,比如对于某个hypothesis是bad data,对于另一个它可能也是。这就要求我们将这个union bound继续压缩。
利用2D的perceptron learning algorithm来举例,如果N = 1,也就是我们只有一个样本,那么它要么是正要么是负,虽然平面上有无数条线,但是似乎只有这么两个效果,也就是只有这么两类线,在这两类线上,它们的$E_ {in}$是一致的。
同样的道理,如果平面上有两个点,我们利用平面上的直线最多也就只能分成4种情况,我们将每一种情况称为一个dichotomy。
当N为3的时候,在纸上我们可以画出,平面上可以有8种dichotomy,但是也会有意外,例如如果3个点拍成一条直线,那么“× ○ ×”的情况,我们似乎无法用一条直线分开了。
当N为4的时候,即使4个点是每一个点都是凸四边形的顶点,我们依然无法将所有的情况都表示出来,如下面这种情况:
× ○
○ ×
实际上,当N为4的时候,我们可以分出来的dichotomy共有14种。而所有的情况有$2^4=16$种,很明显可以看出dichotomy的数量是少于$2^N$。
我们将某个大小为N的dataset所有情况都可以用这个H做出来(dichotomy的数量为$2^N$),成为被H shatter。
当N>4的时候,这个dichotomy又有多少?现在我们很难找到2d perceptron其中这个规律。幸运的是最后我们也不需要关注它具体是多少。
在这里我们考虑几种不同的简单的H,来更加熟悉这个概念:
- Positive Ray
样本为1维的点,这个hypothesis set是在直线上所有的非样本点,选取一个点,该点坐标之前的为positive,之后的为negative。容易看出来,当样本个数为N时候,最多可以有N+1个dichotomy(N个点将该轴分为N+1个部分,每个部分的点是一类)。
- Positive Intervals
样本依然是1维的点,这个hypothesis set是选取一个范围,范围内的为positive,范围之外的为negative。当样本个数为N的时候,最多可以有$\frac {(N+1)N} {2}+1$个dichotomy(N个点将该轴分为N+1个部分,从N+1个部分中任两个取一个点即可,但是这样还缺一种,就是全是positive的情况,我们依然可以做到将这个情况,只需要将两次的点选在同一个部分即可)。
- Convex Sets
样本是二维的点,并且是凸N边形的顶点。选取一个凸多边形的范围,使得多边形内部为positive,外部为negative。可以看到任何时候这个dataset都可以被H shatter,所以它的dichotomy个数是$2^N$.
- 1D perceptron(positive/negative ray)
与1类似,除了最端点的两个部分,其他的分割之后都有个与之对立的dichotomy,而端点的部分得到的是全p或者全n,所有是$2(N+1-2)+2 = 2N$.
而这个2N,N+1等等,我们乘其为成长函数。假设我们希望用$m_H$来代替乘进去的那个集合的大小,用$m_H(N)$来表示成长函数,例如:对于positive ray来说,$m_H(N) = N+1$。
Break Point
我们引入一个新的定义,叫做Break Point,它表示第一个所有情况下都不能被shatter的样本个数。我们将break point简写为k,举个例子,positive ray的k = 2,因为$2+1!=2^2$,同样的道理,positive intervals的k = 3,1D perceptron的k = 3,convex sets的k不存在。
如果用2D perceptron为例,他的k = 4,但是我们很难得到它的成长函数。我们希望它的成长函数可以是一个多项式,这样随着N的增加,$E_ {in}$与$E_ {out}$还是会很大可能相差不多的。
找不到成长函数,另一个希望是可以找到成长函数的上限。比如,在k = 4的情况下,N个样本最多能产生几个dichotomy?我们将这个简写为B(N,k).
k = 4,意味着任意3个样本都不能被shatter。我们试图去填写下面这样的一个表格:
B(N,k)|1|2|3|4|5|…|N
—|:–:|:–:|:–:|:–:|:–:|:–:
1|1|2|2|2|2|…|2
2|1|3|4|4|4|…|4
3|1| |7|8|8|…|8
4|1| | |15|16|…|16
5|1| | | |31|…|32
表格中的已经填写的部分我们很容易就知道了,如果N < k,那么可以shatter,答案就是$2^N$,如果N = k,那么恰好不能shatter,所以最多就是$2^N-1$,接下来我们尝试一个简单的,N = 3,k = 2的情况。我们一个个列举所看到的情况,很容易发现最多最多,可以写出4个dichotomy,任意两个都没有被shatter,如下:
o o o
o o x
o x x
x o o
我们再添加任何一种,都会导致有两个样本被shatter。
将 4 填入表中后,我们发现了一个有趣的规律,在已经填好的数据里,任何一个$B(N,k) = B(N-1,k)+B(N-1,k-1)$,不知道这是否是个巧合?
利用程序$^{见p.s1.}$将B(4,3)的情况跑出来,发现B(4,3)=11:
1 | 11 |
我们将0标为negative,1标为positive,经过整理可以得到下面的样子:
2α
$$
\begin{Bmatrix}
X & X & X & X \
X & X & X & O \
X & X & O & X \
X & X & O & O \
X & O & X & X \
X & O & X & O \
O & X & X & X \
O & X & X & O
\end{Bmatrix}
$$
β
$$
\begin{Bmatrix}
O & O & X & X \
O & X & O & X \
X & O & O & X
\end{Bmatrix}
$$
首先,前2α中每一组种每个dichotomy前3个是一致的,因此只看前3列,$\alpha + \beta \leq B(3,3)$,再看前α组的第一行的前3个,它们每两个必然不能shatter,否则加上第四列的就会出现3个样本被shatter的情况,因此$\alpha \leq B(3,2)$.
总的来说共有$2\alpha + \beta$种,它是小于等于B(3,3)+B(3,2)的。推广到更大的N,这个也依然是成立的,我简单说明一下其中的道理:
B(N-1,k-1)的dichotomy每个后面都增加一个O或者X,那么个数会翻倍,而且可以shatter的样本个数加一,这就是B(N,k)的一部分,其余部分的前N-1个元素不会出现相同的情况,如果相同,则前N-1个元素与之前的2*B(N-1,k-1)个必然会有k-1个被shatter,加上最后的一列会有k个被shatter,这与前提是矛盾的,而且剩余的个数是小于$B(N-1,k) - B(N-1,k-1)$的,不然依然会与条件矛盾。
因此,我们可以填满这张表格了:
B(N,k)|1|2|3|4|5|…|N
—|:–:|:–:|:–:|:–:|:–:|:–:
1|1|2|2|2|2|…|2
2|1|3|4|4|4|…|4
3|1|4|7|8|8|…|8
4|1|5|11|15|16|…|16
5|1|6|16|26|31|…|32
那么B(N,k) = B(N-1,k-1) +B(N-1,k) ,利用上面的表格一路上去,我们可以使用数学归纳法证明下式成立:
$$
B(N,k) \leq \sum _ {i=0} ^{k-1} C_N^i
$$
实际上等号也是成立的,但是证明需要更加复杂的数学理论。
而$C_N^i$的上限是$N^i$,那么$B(N,k)$首项最高项就是$N^{k-1}$,这是一个好消息,因为它的增长速度不够快。所以$m_H(N)$我们可以使用$N^{k-1}$来代替了(当$N \leq 2,k \leq 3$时)。
但是它能否直接带入原来的不等式呢?还是有点问题,实际上,我们无法保证
$$
P[∃h \ln H s.t. |E_ {in}(h) - E_ {out}(h)|>\epsilon] \leq 2 m_H(N) e^{-2\epsilon ^2N}
$$
我们最终得到的是下面的样子:
$$
P[∃h \ln H s.t. |E_ {in}(h) - E_ {out}(h)|>\epsilon] \leq 2 \cdot 2 m_H(2N) \cdot e^{-2 \cdot \frac 1 {16} \epsilon ^2 N}
$$
严格的证明需要很高的数学技巧以及数学理论,但是可以从以下3个方向简单解释下原因:
1. finite $E_ {in}$ and infinite $E_ {out}$
我们的这些证明都是在只考虑了$E_ {in}$的基础上,在泛化的过程中是有问题的。首先,对于dataset,$E_ {in}$的个数是有限的,因为只要有break point,我们一定可以根据N与k找到h种类的上限,但是$E_ {out}$的个数是无限的。虽然同一类h它们的$E_ {in}$可能一致,但是它们的$E_ {out}$并不一致。
如何对付这个无限的$E_ {out}$?我们可以再从总体种抽出一个数目为N的dataset,它用H得到的错误率记为$E’_ {in}$,然后我们用$E_ {in}$与$E’_ {in}$来解决这个问题,因为同样,$E’_ {in}的个数是有限的$。
从下图中可以看出来,当$|E_ {in}-E_ {out}| \geq \epsilon$时候,$|E_ {in}-E’_ {in}| \geq \epsilon$的概率大概为1/2,当然可能会更大。
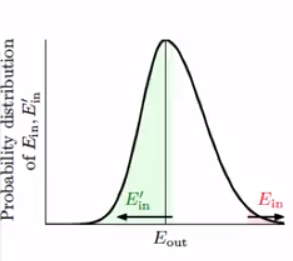
不过实际上的其他情况下,$|E_ {in}-E’_ {in}| \geq \epsilon$也是有可能会发生的,因此
$$
\frac 1 2 P[∃h \ln H s.t. |E_ {in}(h) - E_ {out}(h)| > \epsilon] \leq P[∃h \ln H s.t. |E_ {in}(h) - E’_ {in}(h)| > \frac {\epsilon} 2]
$$
为什么要对${\epsilon}$除以2,我也不清楚。$E_ {out}$是无限的,如果$E_ {out}$与$E_ {in}$是一一对应的关系,那么不除以二上式也是成立的。也许因为是更严格的数学限制,但是不管怎么说经过复杂的数学证明(超出我的能力界限,交给统计学家与数学家吧),上式一定是成立的。
因此我们将无限的换成了有限的,这样离终点就进了一步。我们可以携程下面的样子:
$P[Baddata] \leq 2P[∃h \ln H s.t. |E_ {in}(h) - E’_ {in}(h)| > \frac {\epsilon} 2]$
2. decompose H by kind
这一步,需要使用$m_H(N)$来处理上式的$∃h \ln H$,但是值得注意的是,因为我们后来又取了N个样本来做$E’_ {in}$,因此所有的样本量是2N,需要替换为$m_H(2N)$,得到下面的结果:
$P[Baddata] \leq 2 m_H(2N) P[fixed h s.t. |E_ {in}(h) - E’_ {in}(h)| > \frac {\epsilon} 2]$
3. hoeffding without replacement
第三个,就要用来处理$P[fixed h s.t. |E_ {in}(h) - E’_ {in}(h)| > \frac {\epsilon} 2]$了。实际上,我们可以将上式写成下面的样子:
$$
P[fixed h s.t. |E_ {in}(h) - \frac {E’_ {in}(h)+E_ {in}(h)} 2 | > \frac {\epsilon} 4 ]
$$
仔细观察,上面其实就是hoeffding不等式的一种,只不过这时候的bin不是无限大了,但是最后结果是一样的。(从2N个抽出N个,算出错误的比率,与实际上2N的错误的比率的差)(实际上我对这个解释是存有疑虑的,这个随机抽出2N个应该是从整体出发的,而不是从2N个中抽出来N个,算这个期望差,也许可以从数学上证明二者概率是一致的吧)。
代入hoeffding不等式可以得到最终的结果:
$$
P[∃h \ln H s.t. |E_ {in}(h) - E_ {out}(h)|>\epsilon] \leq 2 \cdot 2 m_H(2N) \cdot e^{-2 \cdot \frac 1 {16} \epsilon ^2 N}
$$
这就是对怎么得到最终结果的简单的说明。严格的证明是非常复杂的。不过我们好歹似乎明白了那么一点点其中的道理。
VC bound
上面的简单证明得到的结果,叫做Vapnik Chervonenkis Bound,简称为VC bound。
引入一个新的定义,叫做VC dimension,它的定义与break point非常类似,VC dimension = k - 1,也就是最后一个可以在某种dataset下被shatter的dataset的大小。
现在我们尝试推算一下 perceptrons 的 VC dimension.
对于1维的来说很简单, 它的VC dimension 是 2.
对于2维的来说,由之前的也可以得到是 3.
那么对于d维的perceptron,我们可以猜测,它的vc dimension 难道是 d+1吗?
为了证明V(d) = d+1,我们需要证明两点:1. $V(d) \geq d+1$ 2. $ V(d) \leq d+1$.
证明$V(d) \geq d+1$:
首先,构造下面一个d+1*d+1的矩阵:
$$
\begin{bmatrix}
1&0&0&0&0&…&0 \
1&1&0&0&0&…&0 \
1&0&1&0&0&…&0 \
…\
1&0&0&0&0&…&1
\end{bmatrix}
$$
上述矩阵每一行都是一个样本的,是d维的,不过会加上额外的$x_0$维度。
共有d+1个样本。
回想perceptron,$XW = Y$(在本例中),而上述矩阵是可逆的,则$W = YX_ {-1}$,因此不管Y怎么变,都有W可以使得它成立,因此至少上面的这个dataset可以被H shatter,所有$V(d) \geq d+1$.
证明$V(d) \leq d+1$:
为了证明上式,我们要再加入一个样本,证明无论如何d+2个样本是不能被shatter的。
我们再上面的矩阵里再加一个非零的行向量$X_ {d+2}$,那么由线性代数可以知道:
$$
X_ {d+2} = \sum _ {i = 1}^{d+1} a_iX_i
$$
因此 $X_ {d+2}W = \sum _ {i = 1}^{d+1} a_iX_iW$.
则 y = ${sign(a_1),sign(a_2),…sign(a_ {d+1}) ,-1 }$这种情况就一定是不能生成的($a_iX_iW$后每一项都是大于等于0的)。
所以d+2个样本是无法被shatter的.
如果前d+1个样本都不能被shatter,就更不用说d+2个可以被shatter了。
所以我们可以得到,V(d) = d+1.
VC dimension 实际上是自由度,一般来说,它是互不依赖的可以变动的参数个数(并不一定总是这样)。
Interpreting of VC dimension
Hoeffding 告诉我们坏事情发生的概率,我们现在反推,好事情发生的概率,很简单如下:
$P[|E_ {in}(g) - E_ {out}(g)|< \epsilon ] \geq 1 - 4(2N)^{d_ {vc} }e^{- \frac 1 8 \epsilon ^2 N} $
如果将大于等于后复杂的那一部分(VC bound)列为$\delta$,那么经过推算可以得到:
$$
\epsilon = \sqrt {\frac 8 N \ln {(\frac {4(2N)^{d_ {vc} } } {\delta })} }
$$
那么我们可以在$1 - \delta$的概率下获得保证$E_ {out}$在这个范围内:
$$
\left [ E_ {in}(g) - \sqrt {\frac 8 N \ln {(\frac {4(2N)^{d_ {vc} } } {\delta })} }, E_ {in}(g) + \sqrt {\frac 8 N \ln {(\frac {4(2N)^{d_ {vc} } } {\delta })} } \right ]
$$
我们比较重视右边的部分,也就是$E_ {out}$最坏是多少。我们称$\sqrt {…}$为penalty for model complexity,记为${\Omega (N,H,\delta)}$.
一般来说,有个以下的关系图:

从上面可以看出来,如果样本个数一定而且保证很高的probability,一味增加维度(增加新的特征)可能会出现过拟合的情况,因为它增加了模型复杂度。这启发了我们在机器学习时候不一定非要增加过多的特征量,或者一味地去降低$E_ {in}$,从而导致泛化能力不强。
此外,我们还需要注意一点,如果我们利用VC bound去求所需要的数据量,往往得到一个很大的值,但是实际上一般来说只要10$d_ {vc}$就差不多足够了,这说明VC bound是很宽松的。因为我们一直取的都是上限,但是我们也很难在包容这么多分布的情况下找到一个更好的界限。
到这里,就说的差不多了,我们证明了如果有VC dimension,那么在N足够大的情况,可以取得不错的学习效果。同时也启发了以后我们在机器学习上的一些做法。
p.s.
- 用程序生成B(4,3),我使用的是很简单的程序,但是应该可以证明这样生成的dichotomy个数就是最大的个数。程序如下:
1 | def check(result,l): |
- hoeffding不等式是无需知道数据分布情况的,也就是对于任何分布它都适用,这也是为何VC bound很宽松的一个原因。