机器学习——PLA算法实现与可视化

上次主要是证明了PLA算法的可行性，这次用来实现PLA算法，并且实现可视化。
这个算法的实现是比较简单的，比较难的部分在于要考虑可视化。

我选择python来实现这个算法，同时利用了matplotlib来进行图形的绘制。
为了可视化数据，我们需要的就不能是仅仅实现那么简单吗，而且还要考虑到可视化之后的清晰与美观。因此这部分的代码主要分成3个部分：

随机生成数据

数据的生成一定是要局限在某个范围内，为了简便我选择的数据特征量范围在0，20之间。而一维数据较为简单，高维数据画不出来，因此生成数据应该是二维或者三维的，以便于可视化。为了简便，我选择生成二维数据。
同时还要生成一组参数，作为$W_f$，也就是最初的规则，这里需要注意，随机生成的参数确定的分割线可能不会经过上述范围的数据，这样导致所有的样本都归为一类，这就失去了可视化的意义，因为生成参数时，我选择了在范围内随机生成两个点，用这两个点来确定分割线，再计算出对应的参数出来。

PLA算法

pla算法没什么好说的，参数初始设为0，然后每次遇到一个坏点，就开始更正，直到没有坏点。我们需要保证传入的数据是线性可分的。

可视化

可视化使用matplotlib来实现，使用两种不同的标志（尽量区分颜色，如红x与绿o）来区分正负样本，在坐标轴上标出，并且用实线来绘制实际的规则，用虚线来绘制我们算法得到的规则。最后可以得到很明显的可视化效果。

可视化结果

随机样本为20个：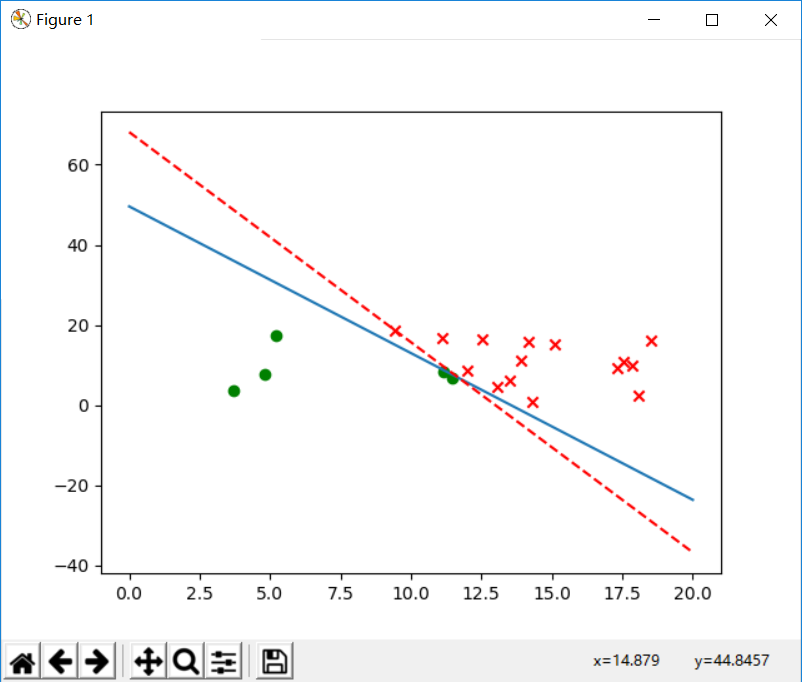

修正次数： 3209

随机样本为50个：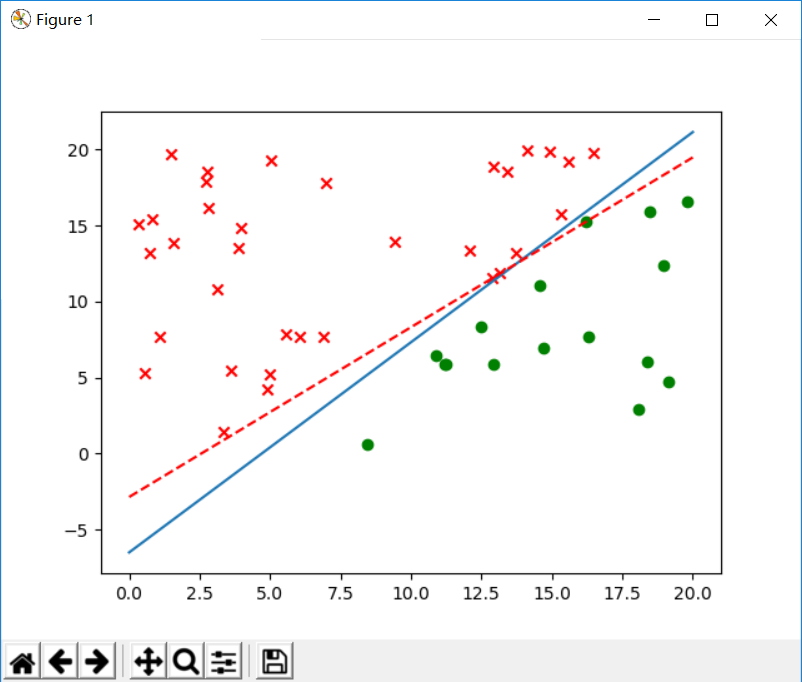

修正次数： 2268

随机样本为100个：

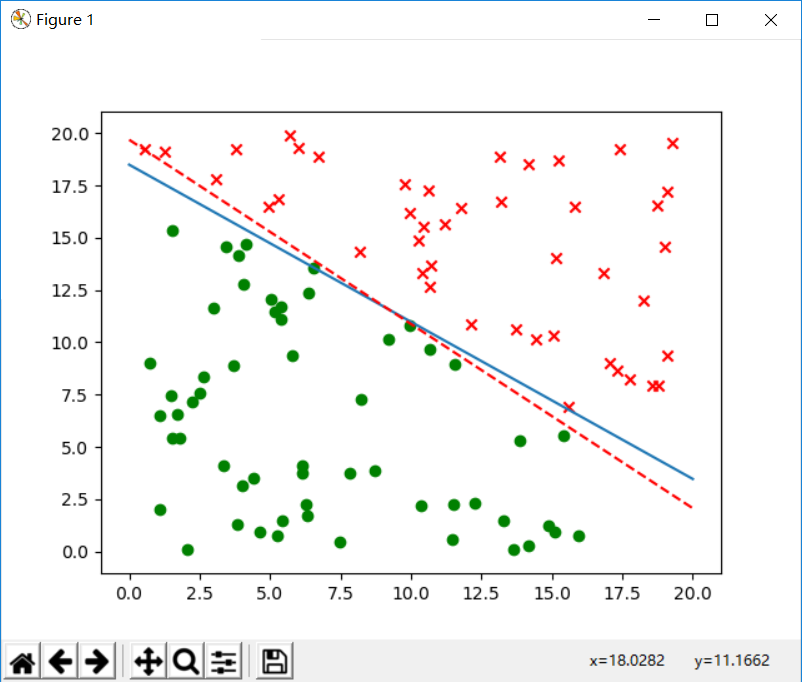
修正次数： 4540

从图中可以看到虽然红线不一定与蓝线重合，但是依然很好的分割了样本。实际上相重合是很困难的，样本越是多越更有可能相似，如下图，样本次数提高到1000，我们可以说推断的规则与原先的规则已经基本一致了。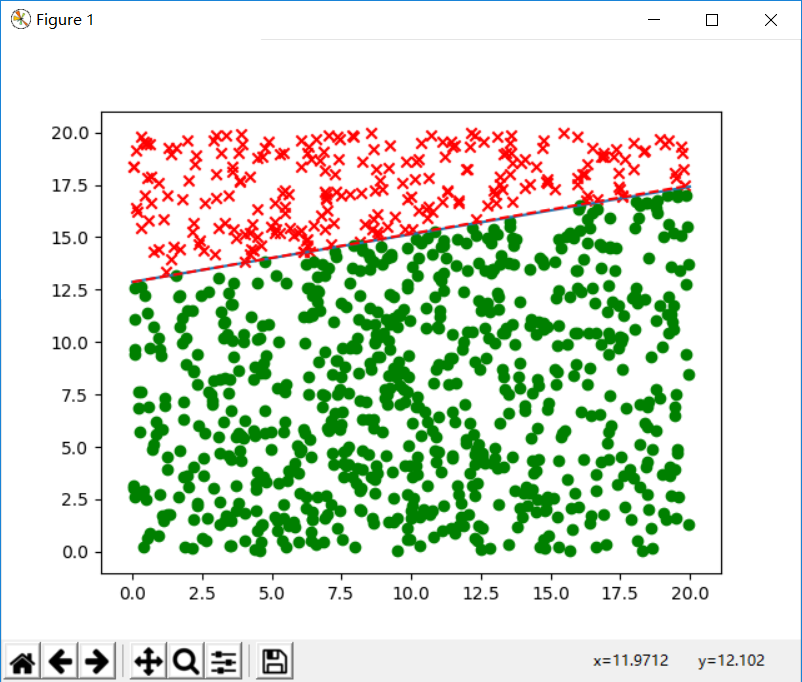

我们从这里看不到修正次数与样本个数之间的关系，因为本来他们关系就不够大，甚至一定程度上可以说是”运气”，但是算法终究会停止，由上一篇博客的证明也可知道，如果R与P的比值很小，那么就算数据再大，也可以很快的得到想要的规则。

下面是PLA实现的代码：

def pla(datas):
    size = len(datas)
    if size<=1:
        return;
    err_i = -1

    dms = len(datas[0])
    if dms == 0:
        return;
    para = [0 for x in range(0,dms)]
    run_times = 0
    while True:

        run_times+=1
        for i in range(0, size):
            p = 0
            for x in range(0, dms - 1):
                p += para[x] * datas[i][x]
            p += para[-1]
            if p <= 0 and datas[i][-1] > 0 or p >= 0 and datas[i][-1] < 0:#ignore datas[i][-1] == 0
                err_i = i;
                break;
        if err_i != -1:
            for x in range(0, dms - 1):
                para[x] += datas[err_i][-1] * datas[err_i][x]  # update the parameters
            para[-1] += datas[err_i][-1]
            err_i = -1;
        else:break;

    return [para,run_times]

全部python代码可以在PLA找到。